SUMERGIRSE EN LA LIBRERIA NUMPY

 Fuente: https://aprendeconalf.es/docencia/python/manual/numpy/

La librería Numpy

NumPy es una librería de Python especializada en el cálculo numérico y el análisis de datos, especialmente para un gran volumen de datos.

Incorpora una nueva clase de objetos llamados arrays que permite representar colecciones de datos de un mismo tipo en varias dimensiones, y funciones muy eficientes para su manipulación.

La ventaja de Numpy frente a las listas predefinidas en Python es que el procesamiento de los arrays se realiza mucho más rápido (hasta 50 veces más) que las listas, lo cual la hace ideal para el procesamiento de vectores y matrices de grandes dimensiones.

La clase de objetos array

Un array es una estructura de datos de un mismo tipo organizada en forma de tabla o cuadrícula de distintas dimensiones.

Las dimensiones de un array también se conocen como ejes.

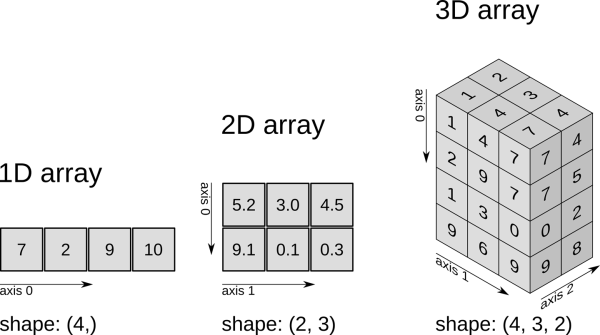
Creación de arrays

Para crear un array se utiliza la siguiente función de NumPy

• np.array(lista) : Crea un array a partir de la lista o tupla lista y devuelve una referencia a él. El número de dimensiones del array dependerá de las listas o tuplas anidadas en lista:

• Para una lista de valores se crea un array de una dimensión, también conocido como vector.

• Para una lista de listas de valores se crea un array de dos dimensiones, también conocido como matriz.

• Para una lista de listas de listas de valores se crea un array de tres dimensiones, también conocido como cubo.

• Y así sucesivamente. No hay límite en el número de dimensiones del array más allá de la memoria disponible en el sistema.

Los elementos de la lista o tupla deben ser del mismo tipo.

>>> # Array de una dimensión
>>> a1 = np.array([1, 2, 3])
>>> print(a1)
[1 2 3]
>>> # Array de dos dimensiones
>>> a2 = np.array([[1, 2, 3], [4, 5, 6]])
>>> print(a2)
[[1 2 3]
 [4 5 6]]
>>> # Array de tres dimensiones
>>> a3 = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
>>> print(a3)
[[[ 1  2  3]
  [ 4  5  6]]

 [[ 7  8  9]
  [10 11 12]]]

Otras funciones útiles que permiten generar arrays son:

• np.empty(dimensiones) : Crea y devuelve una referencia a un array vacío con las dimensiones especificadas en la tupla dimensiones.

• np.zeros(dimensiones) : Crea y devuelve una referencia a un array con las dimensiones especificadas en la tupla dimensiones cuyos elementos son todos ceros.

• np.ones(dimensiones) : Crea y devuelve una referencia a un array con las dimensiones especificadas en la tupla dimensiones cuyos elementos son todos unos.

• np.full(dimensiones, valor) : Crea y devuelve una referencia a un array con las dimensiones especificadas en la tupla dimensiones cuyos elementos son todos valor.

• np.identity(n) : Crea y devuelve una referencia a la matriz identidad de dimensión n.

• np.arange(inicio, fin, salto) : Crea y devuelve una referencia a un array de una dimensión cuyos elementos son la secuencia desde inicio hasta fin tomando valores cada salto.

• np.linspace(inicio, fin, n) : Crea y devuelve una referencia a un array de una dimensión cuyos elementos son la secuencia de n valores equidistantes desde inicio hasta fin.

• np.random.random(dimensiones) : Crea y devuelve una referencia a un array con las dimensiones especificadas en la tupla dimensiones cuyos elementos son aleatorios.

>>> print(np.zeros(3,2))
[[0. 0. 0.]
 [0. 0. 0.]]
>>> print(np.idendity(3))
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
>>> print(np.arange(1, 10, 2))
[1 3 5 7 9]
>>> print(np.linspace(0, 10, 5))
[ 0.   2.5  5.   7.5 10. ]

Atributos de un array

Existen varios atributos y funciones que describen las características de un array.

• a.ndim : Devuelve el número de dimensiones del array a.

• a.shape : Devuelve una tupla con las dimensiones del array a.

• a.size : Devuelve el número de elementos del array a.

• a.dtype: Devuelve el tipo de datos de los elementos del array a.

Acceso a los elementos de un array

Para acceder a los elementos contenidos en un array se usan índices al igual que para acceder a los elementos de una lista, pero indicando los índices de cada dimensión separados por comas.

Al igual que para listas, los índices de cada dimensión comienzan en 0.

También es posible obtener subarrays con el operador dos puntos : indicando el índice inicial y el siguiente al final para cada dimensión, de nuevo separados por comas.

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> print(a[1, 0])  # Acceso al elemento de la fila 1 columna 0
4
>>> print(a[1][0])  # Otra forma de acceder al mismo elemento
4
>>> print(a[:, 0:2])
[[1 2]
 [4 5]]

Filtrado de elementos de un array

Una característica muy útil de los arrays es que es muy fácil obtener otro array con los elementos que cumplen una condición.

• a[condicion] : Devuelve una lista con los elementos del array a que cumplen la condición condicion.

  >>> a = np.array([[1, 2, 3], [4, 5, 6]])
  >>> print(a[(a % 2 == 0)])
  [2 4 6]
  >>> print(a[(a % 2 == 0) &  (a > 2)])
  [2 4]
  

Operaciones matemáticas con arrays

Existen dos formas de realizar operaciones matemáticas con arrays: a nivel de elemento y a nivel de array.

Las operaciones a nivel de elemento operan los elementos que ocupan la misma posición en dos arrays. Se necesitan, por tanto, dos arrays con las mismas dimensiones y el resultado es una array de la misma dimensión.

Los operadores mamemáticos +, -, *, /, %, ** se utilizan para la realizar suma, resta, producto, cociente, resto y potencia a nivel de elemento.

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[1, 1, 1], [2, 2, 2]])
>>> print(a + b )
[[2 3 4]
 [6 7 8]]
>>> print(a / b)
[[1.  2.  3. ]
 [2.  2.5 3. ]]
>>> print(a ** 2)
[[ 1  4  9]
 [16 25 36]]

Álgebra matricial

Numpy incorpora funciones para realizar las principales operaciones algebraicas con vectores y matrices. La mayoría de los métodos algebráicos se agrupan en el submódulo linalg.

Producto escalar de dos vectores

Para realizar el producto escalar de dos vectores se utiliza el operador @ o el siguiente método:

• u.dot(v): Devuelve el producto escalar de los vectores u y v.

  >>> import numpy as np
  >>> a = np.array([1, 2, 3])
  >>> b = np.array([1, 0, 1])
  >>> print(a @ b)
  4
  >>> print(a.dot(b))
  4
  

Módulo de un vector

Para calcular el módulo de un vector se utiliza el siguiente método:

• norm(v): Devuelve el módulo del vector v.

  >>> import numpy as np
  >>> a = np.array([3, 4])
  >>> print(np.linalg.norm(a))
  5.0
  

Producto de dos matrices

Para realizar el producto matricial se utiliza el mismo operador @ y método que para el producto escalar de vectores:

• a.dot(b) : Devuelve el producto matricial de las matrices a y b siempre y cuando sus dimensiones sean compatibles.

  >>> import numpy as np
  >>> a = np.array([[1, 2, 3], [4, 5, 6]])
  >>> b = np.array([[1, 1], [2, 2], [3, 3]])
  >>> print(a @ b)
  [[14 14]
  [32 32]]
  >>> print(a.dot(b))
  [[14 14]
  [32 32]]
  

Matriz traspuesta

Para trasponer una matriz se utiliza el método

• a.T : Devuelve la matriz traspuesta de la matriz a.

  >>> import numpy as np
  >>> a = np.array([[1, 2, 3], [4, 5, 6]])
  >>> print(a.T)
  [[1 4]
  [2 5]
  [3 6]]
  

Traza de una matriz

La traza de una matriz cuadrada se calcula con el siguiente método:

• a.trace() : Devuelve la traza (suma de la diagonal principal) de la matriz cuadrada a.

  >>> import numpy as np
  >>> a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
  >>> print(a.trace())
  15
  

Determinante de una matriz

El determinante de una matriz cuadrada se calcula con la siguiente función:

• det(a) : Devuelve el determinante de la matriz cuadrada a.

  >>> import numpy as np
  >>> a = np.array([[1, 2], [3, 4]])
  >>> print(np.linalg.det(a))
  -2.0
  

Matriz inversa

La inversa de una matriz se calcula con la siguiente función:

• inv(a) : Devuelve la matriz inversa de la matriz cuadrada a.

  >>> import numpy as np
  >>> a = np.array([[1, 2], [3, 4]])
  >>> print(np.linalg.inv(a))
  [[-2.   1. ]
  [ 1.5 -0.5]]
  

Autovalores de una matriz

Los autovalores de una matriz cuadrada se calculan con la siguiente función:

• eigvals(a) : Devuelve los autovalores de la matriz cuadrada a.

  >>> import numpy as np
  >>> a = np.array([[1, 1, 0], [1, 2, 1], [0, 1, 1]])
  >>> print(np.linalg.eigvals(a))
  [ 3.00000000e+00  1.00000000e+00 -3.36770206e-17]
  

Autovectores de una matriz

Los autovectores de una matriz cuadrada se calculan con la siguiente función:

• eig(a) : Devuelve los autovalores y los autovectores asociados de la matriz cuadrada a.

  >>> import numpy as np
  >>> a = np.array([[1, 1, 0], [1, 2, 1], [0, 1, 1]])
  >>> print(np.linalg.eig(a))
  (array([ 3.00000000e+00,  1.00000000e+00, -3.36770206e-17]), array([[-4.08248290e-01,  7.07106781e-01,  5.77350269e-01],
        [-8.16496581e-01,  2.61239546e-16, -5.77350269e-01],
        [-4.08248290e-01, -7.07106781e-01,  5.77350269e-01]]))
  

Solución de un sistema de ecuaciones

Para resolver un sistema de ecuaciones lineales se utiliza la función siguiente:

• solve(a, b) : Devuelve la solución del sistema de ecuaciones lineales con los coeficientes de la matriz a y los términos independientes de la matriz b.

  >>> import numpy as np
  # Sistema de dos ecuaciones y dos incógnitas
  # x + 2y = 1
  # 3x + 5y = 2 
  >>> a = np.array([[1, 2], [3, 5]])
  >>> b = np.array([1, 2])
  >>> print(np.linalg.solve(a, b))
  [-1.  1.]
  

Numpy