Thinkcspy. Funciones / 6.9 Desarrollo del programa

 

6.9. Desarrollo del programa

En este punto, debería poder mirar las funciones completas y decir qué lo hacen. Además, si ha estado haciendo los ejercicios, ha escrito algunos Pequeñas funciones. Mientras escribe funciones más grandes, puede comenzar a tener más Dificultad, especialmente con tiempo de ejecución y errores semánticos.

Para lidiar con programas cada vez más complejos, vamos a sugerir una técnica llamado desarrollo incremental . El objetivo del desarrollo incremental es Evite las largas sesiones de depuración agregando y probando solo una pequeña cantidad de código a la vez.

Como ejemplo, suponga que desea encontrar la distancia entre dos puntos, dada por las coordenadas (x ₁ , y ₁ ) y (x ₂ , y ₂ ). Por el teorema pitagórico, la distancia es:

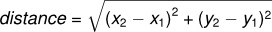
El primer paso es considerar qué distance la función debería parecer en Pitón. En otras palabras, ¿cuáles son las entradas (parámetros) y cuál es la salida? (Valor de retorno)?

En este caso, los dos puntos son las entradas, que podemos representar usando cuatro parámetros. El valor de retorno es la distancia, que es un valor de punto flotante.

Ya podemos escribir un esquema de la función que captura nuestro pensamiento hasta ahora. 

 

>>def distance(x1, y1, x2, y2):
>>    return 0.0

Obviamente, esta versión de la función no calcula distancias; siempre Devuelve cero. Pero es sintácticamente correcto, y se ejecutará, lo que significa que podemos probarlo antes de hacerlo más complicado.

Importamos el módulo de prueba para permitirnos escribir una prueba unitaria para la función. 

>>import test
>>def distance(x1, y1, x2, y2):
>>    return 0.0

>>test.testEqual(distance(1, 2, 1, 2), 0)
 

 

El testEqual La función del módulo de prueba llama a la función de distancia con entradas de muestra: (1,2, 1,2). Los primeros 1,2 son las coordenadas del primer punto y el segundo 1,2 son las coordenadas del segundo punto. ¿Cuál es la distancia entre estos dos puntos? Cero. testEqual compara lo que devuelve la función de distancia y el 0 (la respuesta correcta).

Extender el programa ...

En la línea 6, escriba otra prueba unitaria. Use (1,2, 4,6) como parámetros a la función de distancia. ¿Qué tan separados están estos dos puntos? Use ese valor (en lugar de 0) como la respuesta correcta para esta prueba unitaria.

En la línea 7, escriba otra prueba unitaria. Use (0,0, 1,1) como parámetros a la función de distancia. ¿Qué tan separados están estos dos puntos? Use ese valor como la respuesta correcta para esta prueba unitaria.

La primera prueba pasa, pero las otras fallan ya que la función de distancia aún no contiene todos los pasos necesarios.

Al probar una función, es esencial conocer la respuesta correcta.

Para la segunda prueba, la distancia horizontal es igual a 3 y la vertical La distancia es igual a 4; De esa manera, el resultado es 5 (la hipotenusa de un 3-4-5 triángulo). Para la tercera prueba, tenemos un triángulo de 1-1-SQRT (2).

En este punto hemos confirmado que la función es sintácticamente correcta y Podemos comenzar a agregar líneas de código. Después de cada cambio incremental, probamos el funcionar nuevamente. Si se produce un error en algún momento, sabemos dónde debe estar, en La última línea que agregamos.

Un primer paso lógico en el cálculo es encontrar las diferencias x ₂ - x ₁ e y ₂ - y ₁ . Almacenaremos esos valores en variables temporales nombradas dxy dy. 

>>def distance(x1, y1, x2, y2):
>>    dx = x2 - x1
>>    dy = y2 - y1
>>    return 0.0

A continuación, calculamos la suma de cuadrados de dxy dy. 

>>def distance(x1, y1, x2, y2):
>>    dx = x2 - x1
>>    dy = y2 - y1
>>    dsquared = dx**2 + dy**2
>>    return 0.0

 

Nuevamente, podríamos ejecutar el programa en esta etapa y verificar el valor de dsquared (cual debería ser 25).

Finalmente, usando el exponente fraccional 0.5 para encontrar la raíz cuadrada, Calculamos y devolvemos el resultado. 

>>import test
>>def distance(x1, y1, x2, y2):
>>    dx = x2 - x1
>>    dy = y2 - y1
>>    dsquared = dx**2 + dy**2
>>    result = dsquared**0.5
>>    return result

>>test.testEqual(distance(1,2, 1,2), 0)
>>test.testEqual(distance(1,2, 4,6), 5)
>>test.testEqual(distance(0,0, 1,1), 1.41)
 

 

Corrige el error ...

Dos de las pruebas pasan pero la última falla. ¿Todavía hay un error en la función?

Con frecuencia descubrimos errores en las funciones que estamos escribiendo. Sin embargo, es posible que haya un error en una prueba. Aquí el error está en la precisión de la respuesta correcta.

La tercera prueba falla porque, por defecto, prueba TestEqual 5 dígitos a la derecha del punto decimal.

• Cambiar 1.41a 1.41421 y correr. La prueba pasará.

Hay circunstancias en las que 2 dígitos a la derecha del punto decimal son suficientemente precisos.

• Copiar línea 11 en la línea 12. En línea 12, cambiar 1.41421a 1.41. Correr. La prueba falla.

• Tipo , 2 después de 1.41. (El 2 representa la precisión de la prueba: cuántos dígitos a la derecha del decimal debe ser correcto).

¡Ahora las cuatro pruebas pasan! ¡Maravilloso! Sin embargo, es posible que aún necesite realizar pruebas adicionales.

Cuando comience, puede agregar solo una línea o dos de código a la vez. Como tú Obtenga más experiencia, puede encontrarse escribiendo y depurando más grande trozos conceptuales. A medida que mejora sus habilidades de programación, debe encontrarse Gestión de trozos más grandes y más grandes: esto es muy similar a la forma en que aprendimos a leer letras, sílabas, palabras, frases, oraciones, párrafos, etc., o la forma en que aprendemos Para fragmentar la música: desde notas indviduales hasta acordes, bares, frases, etc.

Los aspectos clave del proceso son:

1. Asegúrese de saber lo que está tratando de lograr. Entonces puede escribir pruebas unitarias apropiadas.

2. Comience con un programa de esqueleto que funcione y haga pequeños cambios incrementales. En cualquier Punto, si hay un error, sabrá exactamente dónde está.

3. Use variables temporales para contener valores intermedios para que pueda inspeccionar fácilmente y revisarlos.

4. Una vez que el programa esté funcionando, es posible que desee consolidar múltiples declaraciones en expresiones compuestas, Pero solo haga esto si no hace que el programa sea más difícil de leer.