Ejercicio basico de confiabilidad aplicando Weibull, explicado paso a paso

 

¡Claro! Con gusto te explico paso a paso este bloque de código de Análisis de Weibull utilizando la librería reliability de Python. Este código es un excelente ejemplo de cómo simular, ajustar y visualizar un modelo de confiabilidad.

---

🔍 Explicación Paso a Paso del Código Weibull

El objetivo de este script es simular un conjunto de datos de tiempo hasta la falla, ajustar un modelo de Weibull de 2 parámetros a esos datos, y luego comparar el modelo ajustado con la distribución original.

Paso 1: Importación de Librerías (Líneas 1-3)

Python

from reliability.Distributions import Weibull_Distribution
from reliability.Fitters import Fit_Weibull_2P
from reliability.Probability_plotting import plot_points
import matplotlib.pyplot as plt

• from reliability.Distributions import Weibull_Distribution: Importa la clase para crear una distribución de Weibull con parámetros conocidos (usada para simular el mundo real).

• from reliability.Fitters import Fit_Weibull_2P: Importa la función clave que toma datos de fallas y automáticamente encuentra los mejores parámetros de Weibull de 2 parámetros ($\eta$ (escala) y $\beta$ (forma)).

• from reliability.Probability_plotting import plot_points: Importa una función especializada para trazar los puntos de la data real sobre un gráfico de confiabilidad.

• import matplotlib.pyplot as plt: Importa la librería estándar de Python para crear y personalizar gráficos.

Paso 2: Creación y Simulación de Datos (Líneas 4-5)

Python

dist = Weibull_Distribution(alpha=30, beta=2)  # creates the distribution object
data = dist.random_samples(20, seed=42)  # draws 20 samples from the distribution. Seeded for repeatability

• dist = Weibull_Distribution(alpha=30, beta=2):

  • Crea un objeto de distribución teórica de Weibull.

  • alpha ($\eta$) = 30 (Parámetro de Escala o Vida Característica).

  • beta ($\beta$) = 2 (Parámetro de Forma).

• data = dist.random_samples(20, seed=42):

  • Genera 20 muestras de fallas aleatorias a partir de la distribución teórica (dist). Este es el conjunto de datos simulado que un ingeniero obtendría en un ensayo de vida.

  • seed=42 asegura que si ejecutas el código de nuevo, obtendrás exactamente las mismas 20 muestras, garantizando la repetibilidad del experimento.

Paso 3: Ajuste del Modelo y Gráfico de Probabilidad (Líneas 6-7)

Python

plt.subplot(121)
fit = Fit_Weibull_2P(failures=data)  # fits a Weibull distribution to the data and generates the probability plot

• plt.subplot(121): Indica a Matplotlib que el siguiente gráfico debe colocarse en una cuadrícula de 1 fila, 2 columnas, en la posición 1 (el gráfico de la izquierda).

• fit = Fit_Weibull_2P(failures=data):

  • Esta es la función de análisis central. Toma los datos de fallas (data).

  • Ajusta (encuentra) los mejores parámetros $\eta$ y $\beta$ para la distribución de Weibull que mejor se adapte a estos 20 puntos de datos.

  • Automáticamente genera y muestra el Gráfico de Probabilidad de Weibull en el subplot(121). Este gráfico convierte la data a escala log-log para ver si se ajusta a una línea recta (validando el modelo).

  • El resultado del ajuste (los parámetros, el error estándar, las bandas de confianza) se almacena en el objeto fit.

Paso 4: Trazado de Funciones de Supervivencia (Líneas 8-11)

Esta sección se enfoca en el segundo gráfico, que compara la función de supervivencia (SF, Survival Function).

Python

plt.subplot(122)
fit.distribution.SF(label='fitted distribution')
dist.SF(label='original distribution', linestyle='--')
plot_points(failures=data, func='SF')

• plt.subplot(122): Indica que el siguiente gráfico debe ir en la posición 2 (el gráfico de la derecha).

• fit.distribution.SF(label='fitted distribution'):

  • Accede al objeto de distribución que se ajustó a los datos (almacenado dentro de fit).

  • Traza su Función de Supervivencia (la probabilidad de que el componente sobreviva hasta el tiempo $t$).

• dist.SF(label='original distribution', linestyle='--'):

  • Traza la Función de Supervivencia de la distribución original/teórica (la que usamos para crear los datos en el Paso 2), generalmente como una línea punteada para contrastar.

• plot_points(failures=data, func='SF'):

  • Superpone los puntos de datos reales (data) en el gráfico de SF. Si el ajuste es bueno, estos puntos deben caer cerca de la línea ajustada.

Paso 5: Visualización Final (Líneas 12-13)

Python

plt.legend()
plt.show()

• plt.legend(): Muestra la leyenda de las etiquetas para distinguir entre la distribución ajustada y la original.

• plt.show(): Muestra ambos gráficos generados (el de probabilidad y el de supervivencia).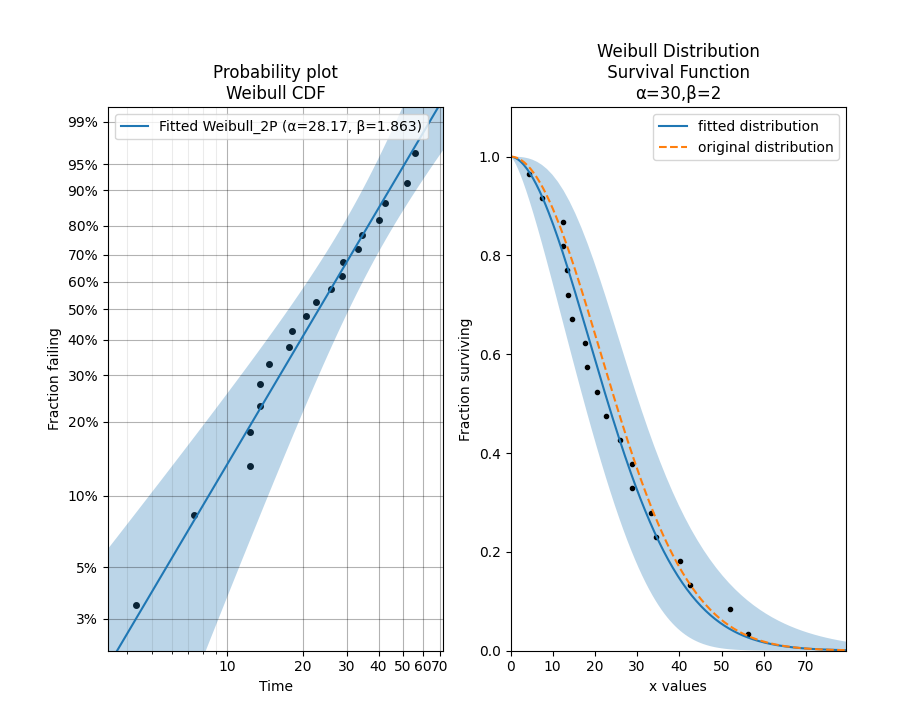

   

   

   

   

---

📊 Interpretación de Resultados

La sección de resultados que proporcionaste es el resumen impreso por la función Fit_Weibull_2P:

Parameter  Point Estimate  Standard Error  Lower CI  Upper CI
  Alpha         28.1696         3.57032   21.9733   36.1131
  Beta         1.86309         0.32449   1.32428   2.62111

• Original (Teórico): $\eta=30$, $\beta=2$.

• Estimado (Ajustado):

  • Alpha ($\eta$) = 28.1696: La vida característica del componente es de aproximadamente 28.17 unidades de tiempo (muy cerca de la $\eta$ teórica de 30).

  • Beta ($\beta$) = 1.86309: El parámetro de forma (tasa de falla creciente) es 1.86, también muy cercano al valor teórico de 2.

El resultado muestra que el modelo de Máxima Verosimilitud (MLE) de Python ha hecho un excelente trabajo al estimar los parámetros verdaderos a partir de solo 20 puntos de datos, confirmando que la librería reliability es muy efectiva para este tipo de análisis.