Inicio rápido¶
Instalación¶
Instalar mediante pip:
pip install lifelines
O
Instalar mediante conda :
conda install -c conda-forge lifelines
Modelos de Kaplan-Meier, Nelson-Aalen y paramétricos¶
Nota
Para los lectores que busquen una introducción al análisis de supervivencia, se recomienda comenzar con Introducción al análisis de supervivencia
Comencemos importando algunos datos. Necesitamos saber la duración de las observaciones de los individuos y si "murieron" o no.
from lifelines.datasets import load_waltons
df = load_waltons() # returns a Pandas DataFrame
print(df.head())
"""
T E group
0 6 1 miR-137
1 13 1 miR-137
2 13 1 miR-137
3 13 1 miR-137
4 19 1 miR-137
"""
T = df['T']
E = df['E']
Tes una matriz de duraciones, Ey es una matriz booleana o binaria que representa si se observó o no la “muerte” (alternativamente, un individuo puede ser censurado). Ajustaremos un modelo de Kaplan-Meier a esto, implementado como KaplanMeierFitter:
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
kmf.fit(T, event_observed=E) # or, more succinctly, kmf.fit(T, E)
Tras llamar al fit()método, tenemos acceso a nuevas propiedades survival_function_y métodos plot(). Este último es una interfaz para la biblioteca de gráficos interna de Pandas.
kmf.survival_function_
kmf.cumulative_density_
kmf.plot_survival_function()
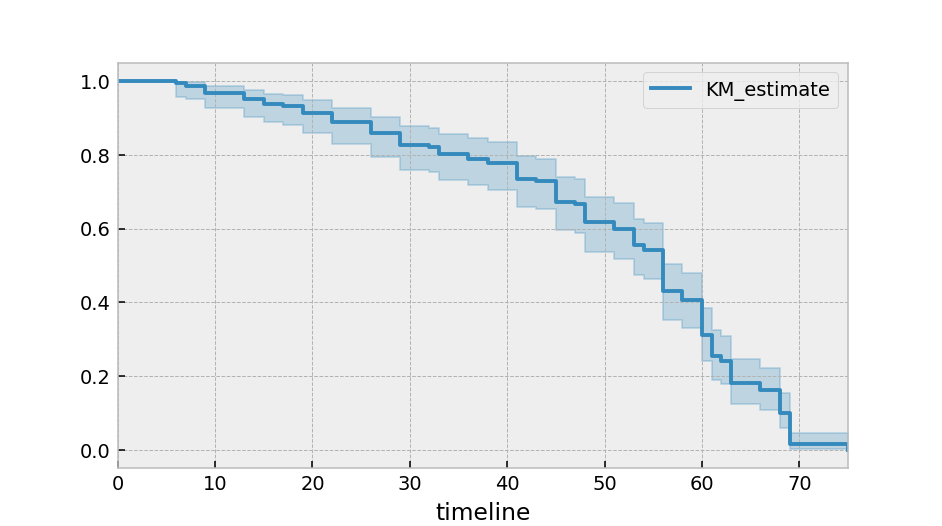
Alternativamente, puede graficar la función de distribución acumulativa:
kmf.plot_cumulative_density()
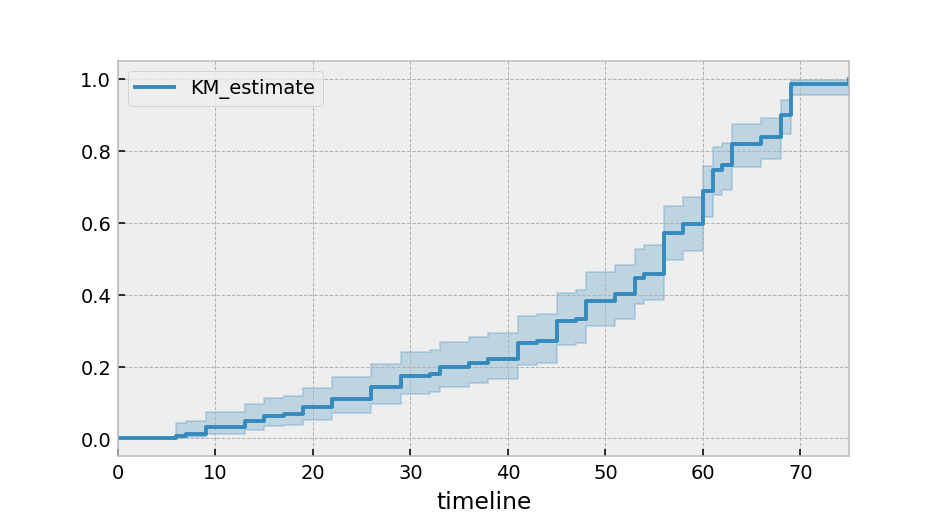
Al especificar el timelineargumento de palabra clave en fit(), podemos cambiar la forma en que se indexan los modelos anteriores:
kmf.fit(T, E, timeline=range(0, 100, 2))
kmf.survival_function_ # index is now the same as range(0, 100, 2)
kmf.confidence_interval_ # index is now the same as range(0, 100, 2)
Un dato estadístico útil para resumir es el tiempo medio de supervivencia, que representa el momento en que ha fallecido el 50% de la población:
from lifelines.utils import median_survival_times
median_ = kmf.median_survival_time_
median_confidence_interval_ = median_survival_times(kmf.confidence_interval_)
En lugar del estimador de Kaplan-Meier, quizás le interese un modelo paramétrico. Lifelines incluye modelos paramétricos predefinidos, como por ejemplo Weibull, Log-Normal, Log-Logístico, entre otros.
import matplotlib.pyplot as plt
import numpy as np
from lifelines import *
fig, axes = plt.subplots(3, 3, figsize=(13.5, 7.5))
kmf = KaplanMeierFitter().fit(T, E, label='KaplanMeierFitter')
wbf = WeibullFitter().fit(T, E, label='WeibullFitter')
exf = ExponentialFitter().fit(T, E, label='ExponentialFitter')
lnf = LogNormalFitter().fit(T, E, label='LogNormalFitter')
llf = LogLogisticFitter().fit(T, E, label='LogLogisticFitter')
pwf = PiecewiseExponentialFitter([40, 60]).fit(T, E, label='PiecewiseExponentialFitter')
ggf = GeneralizedGammaFitter().fit(T, E, label='GeneralizedGammaFitter')
sf = SplineFitter(np.percentile(T.loc[E.astype(bool)], [0, 50, 100])).fit(T, E, label='SplineFitter')
wbf.plot_survival_function(ax=axes[0][0])
exf.plot_survival_function(ax=axes[0][1])
lnf.plot_survival_function(ax=axes[0][2])
kmf.plot_survival_function(ax=axes[1][0])
llf.plot_survival_function(ax=axes[1][1])
pwf.plot_survival_function(ax=axes[1][2])
ggf.plot_survival_function(ax=axes[2][0])
sf.plot_survival_function(ax=axes[2][1])
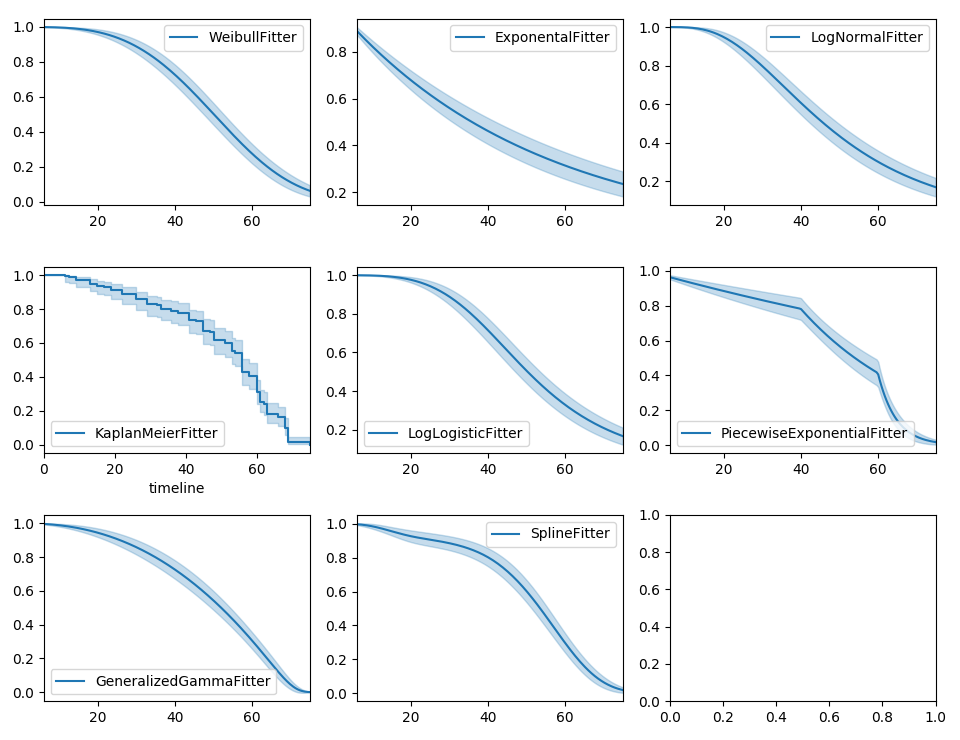
Múltiples grupos¶
groups = df['group']
ix = (groups == 'miR-137')
kmf.fit(T[~ix], E[~ix], label='control')
ax = kmf.plot_survival_function()
kmf.fit(T[ix], E[ix], label='miR-137')
ax = kmf.plot_survival_function(ax=ax)
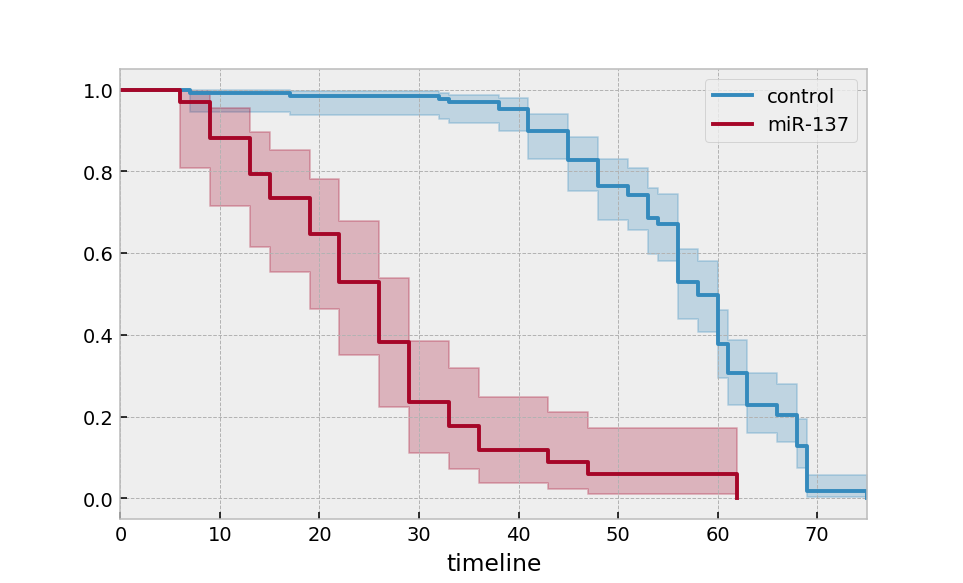
Alternativamente, para muchos más grupos y más "al estilo panda":
ax = plt.subplot(111)
kmf = KaplanMeierFitter()
for name, grouped_df in df.groupby('group'):
kmf.fit(grouped_df["T"], grouped_df["E"], label=name)
kmf.plot_survival_function(ax=ax)
Existe una funcionalidad similar para NelsonAalenFitter:
from lifelines import NelsonAalenFitter
naf = NelsonAalenFitter()
naf.fit(T, event_observed=E)
pero en lugar de que survival_function_se exponga algo, cumulative_hazard_se expone algo.
Nota
Al igual que en Scikit-Learn , todas las cantidades estimadas estadísticamente añaden un guion bajo al nombre de la propiedad.
Nota
En Análisis de supervivencia con líneas de vida se encuentran documentos más detallados sobre la estimación de la función de supervivencia y el riesgo acumulado .
Obtener los datos en el formato correcto¶
A menudo tendrás datos con el siguiente aspecto:
*start_time1*, *end_time1*
*start_time2*, *end_time2*
*start_time3*, None
*start_time4*, *end_time4*
Lifelines dispone de algunas funciones de utilidad para transformar este conjunto de datos en vectores de duración y censura. La más común es lifelines.utils.datetimes_to_durations().
from lifelines.utils import datetimes_to_durations
# start_times is a vector or list of datetime objects or datetime strings
# end_times is a vector or list of (possibly missing) datetime objects or datetime strings
T, E = datetimes_to_durations(start_times, end_times, freq='h')
Quizás le interese ver la tabla de supervivencia dadas ciertas duraciones y vectores de censura. La siguiente función lifelines.utils.survival_table_from_events()le ayudará con ello:
from lifelines.utils import survival_table_from_events
table = survival_table_from_events(T, E)
print(table.head())
"""
removed observed censored entrance at_risk
event_at
0 0 0 0 163 163
6 1 1 0 0 163
7 2 1 1 0 162
9 3 3 0 0 160
13 3 3 0 0 157
"""
regresión de supervivencia¶
Si bien el KaplanMeierFittermodelo anterior es útil, solo nos ofrece una visión «promedio» de la población. A menudo disponemos de datos específicos a nivel individual que nos gustaría utilizar. Para ello, recurrimos a la regresión de supervivencia .
Nota
En Regresión de Supervivencia se encuentran disponibles documentación y tutoriales más detallados .
El conjunto de datos para los modelos de regresión es diferente de los conjuntos de datos anteriores. Todos los datos, incluidas las duraciones, los indicadores censurados y las covariables, deben estar contenidos en un DataFrame de Pandas .
from lifelines.datasets import load_regression_dataset
regression_dataset = load_regression_dataset() # a Pandas DataFrame
Se crea una instancia de un modelo de regresión y se ajusta a un conjunto de datos fit. La columna de duración y la columna de evento se especifican en la llamada a la función fit. A continuación, modelamos nuestro conjunto de datos de regresión utilizando el modelo de riesgos proporcionales de Cox (documentación completa aquí) .
from lifelines import CoxPHFitter
# Using Cox Proportional Hazards model
cph = CoxPHFitter()
cph.fit(regression_dataset, 'T', event_col='E')
cph.print_summary()
"""
<lifelines.CoxPHFitter: fitted with 200 total observations, 11 right-censored observations>
duration col = 'T'
event col = 'E'
baseline estimation = breslow
number of observations = 200
number of events observed = 189
partial log-likelihood = -807.62
time fit was run = 2020-06-21 12:26:28 UTC
---
coef exp(coef) se(coef) coef lower 95% coef upper 95% exp(coef) lower 95% exp(coef) upper 95%
var1 0.22 1.25 0.07 0.08 0.37 1.08 1.44
var2 0.05 1.05 0.08 -0.11 0.21 0.89 1.24
var3 0.22 1.24 0.08 0.07 0.37 1.07 1.44
z p -log2(p)
var1 2.99 <0.005 8.49
var2 0.61 0.54 0.89
var3 2.88 <0.005 7.97
---
Concordance = 0.58
Partial AIC = 1621.24
log-likelihood ratio test = 15.54 on 3 df
-log2(p) of ll-ratio test = 9.47
"""
cph.plot()
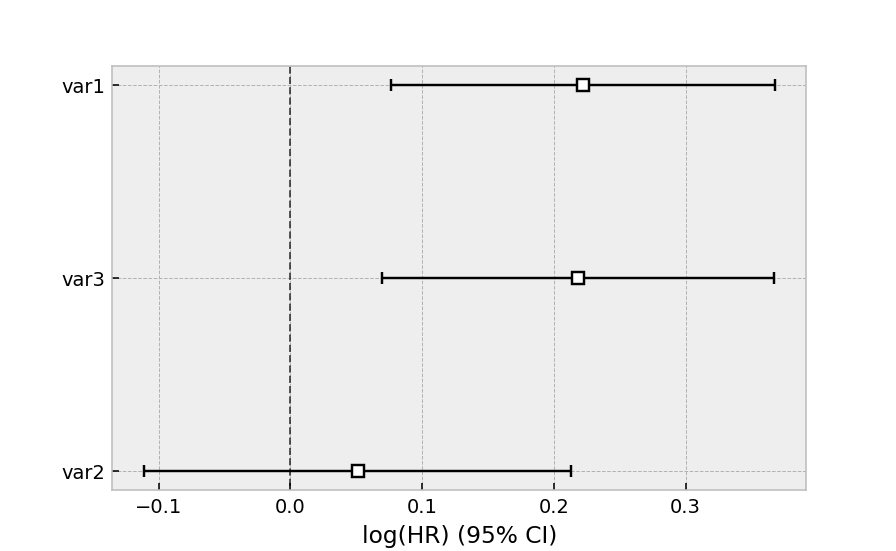
El mismo conjunto de datos, pero con un modelo de tiempo de falla acelerado de Weibull . Este modelo tiene dos parámetros (ver la documentación aquí ), y podemos optar por modelar ambos usando nuestras covariables o solo uno. A continuación, modelamos únicamente el parámetro de escala lambda_.
from lifelines import WeibullAFTFitter
wft = WeibullAFTFitter()
wft.fit(regression_dataset, 'T', event_col='E')
wft.print_summary()
"""
<lifelines.WeibullAFTFitter: fitted with 200 total observations, 11 right-censored observations>
duration col = 'T'
event col = 'E'
number of observations = 200
number of events observed = 189
log-likelihood = -504.48
time fit was run = 2020-06-21 12:27:05 UTC
---
coef exp(coef) se(coef) coef lower 95% coef upper 95% exp(coef) lower 95% exp(coef) upper 95%
lambda_ var1 -0.08 0.92 0.02 -0.13 -0.04 0.88 0.97
var2 -0.02 0.98 0.03 -0.07 0.04 0.93 1.04
var3 -0.08 0.92 0.02 -0.13 -0.03 0.88 0.97
Intercept 2.53 12.57 0.05 2.43 2.63 11.41 13.85
rho_ Intercept 1.09 2.98 0.05 0.99 1.20 2.68 3.32
z p -log2(p)
lambda_ var1 -3.45 <0.005 10.78
var2 -0.56 0.57 0.80
var3 -3.33 <0.005 10.15
Intercept 51.12 <0.005 inf
rho_ Intercept 20.12 <0.005 296.66
---
Concordance = 0.58
AIC = 1018.97
log-likelihood ratio test = 19.73 on 3 df
-log2(p) of ll-ratio test = 12.34
"""
wft.plot()
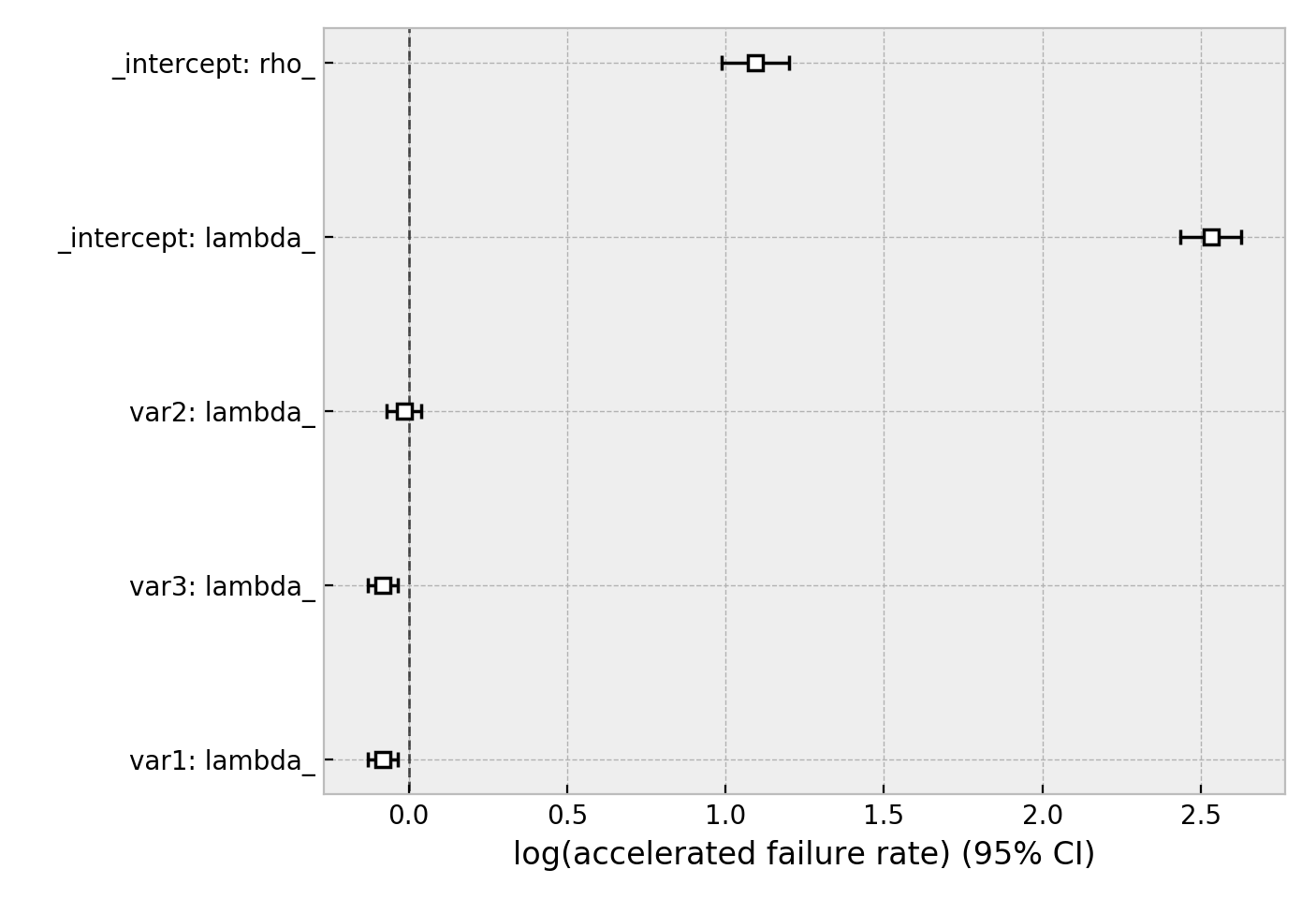
También existen otros modelos AFT, véase aquí . Un modelo de regresión alternativo es el modelo aditivo de Aalen, que presenta riesgos variables en el tiempo:
# Using Aalen's Additive model
from lifelines import AalenAdditiveFitter
aaf = AalenAdditiveFitter(fit_intercept=False)
aaf.fit(regression_dataset, 'T', event_col='E')
Junto con `x` CoxPHFittere `y` WeibullAFTFitter, tras el ajuste tendrás acceso a propiedades como `x` e summary`y` y a métodos como plot` predict_cumulative_hazardsx` e `y` predict_survival_function. Los dos últimos métodos requieren un argumento adicional de covariables:
X = regression_dataset.loc[0]
ax = wft.predict_survival_function(X).rename(columns={0:'WeibullAFT'}).plot()
cph.predict_survival_function(X).rename(columns={0:'CoxPHFitter'}).plot(ax=ax)
aaf.predict_survival_function(X).rename(columns={0:'AalenAdditive'}).plot(ax=ax)
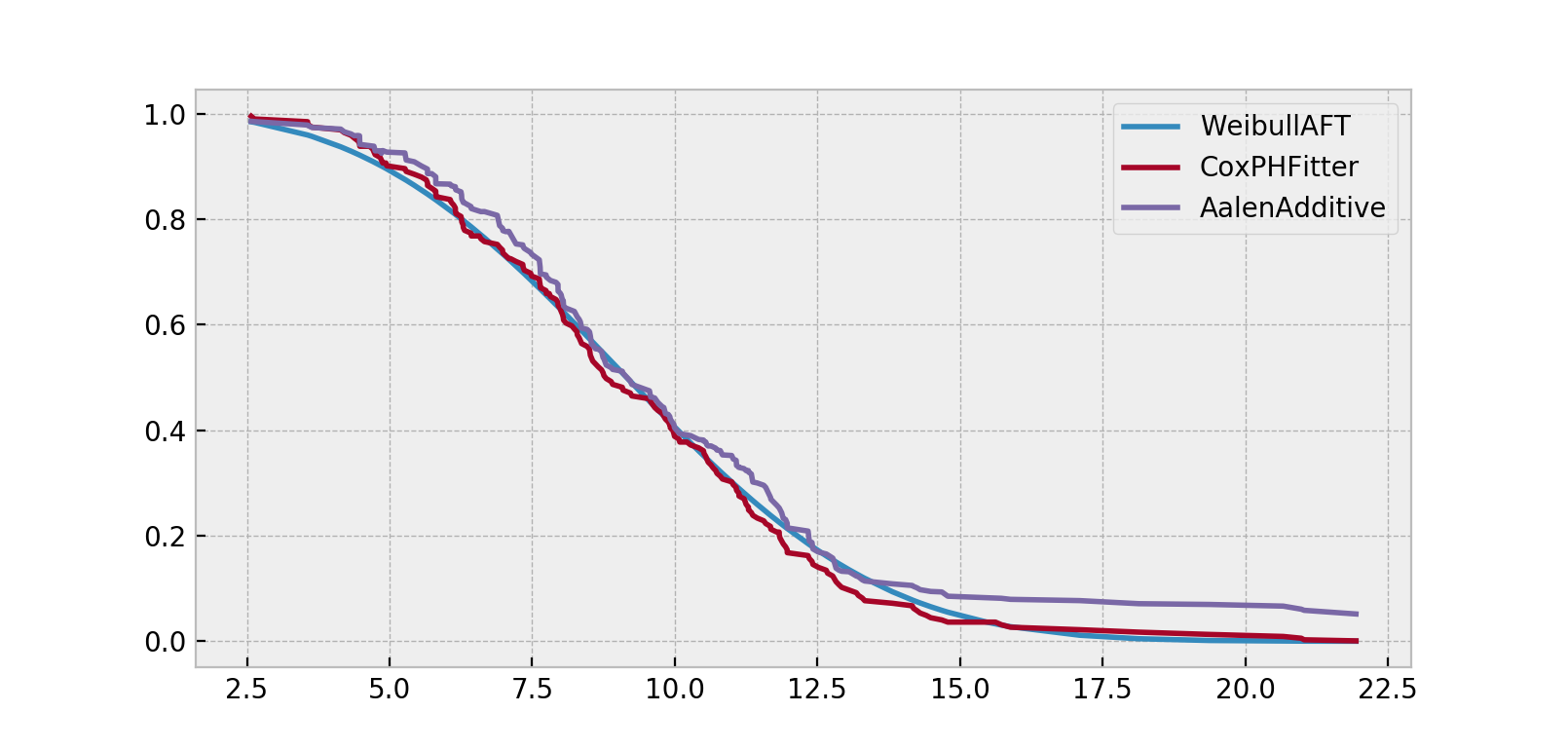
Nota
En Regresión de Supervivencia se encuentran disponibles documentación y tutoriales más detallados .

No hay comentarios.:
Publicar un comentario