Implementar un corrector ortografico en Python

 

from collections import Counter

def words(text): return re.findall(r'\w+', text.lower())

WORDS = Counter(words(open('big.txt').read()))

def P(word, N=sum(WORDS.values())):

"Probability of `word`."

return WORDS[word] / N

def correction(word):

"Most probable spelling correction for word."

return max(candidates(word), key=P)

def candidates(word):

"Generate possible spelling corrections for word."

return (known([word]) or known(edits1(word)) or known(edits2(word)) or [word])

def known(words):

"The subset of `words` that appear in the dictionary of WORDS."

return set(w for w in words if w in WORDS)

def edits1(word):

"All edits that are one edit away from `word`."

letters = 'abcdefghijklmnopqrstuvwxyz'

splits = [(word[:i], word[i:]) for i in range(len(word) + 1)]

deletes = [L + R[1:] for L, R in splits if R]

transposes = [L + R[1] + R[0] + R[2:] for L, R in splits if len(R)>1]

replaces = [L + c + R[1:] for L, R in splits if R for c in letters]

inserts = [L + c + R for L, R in splits for c in letters]

return set(deletes + transposes + replaces + inserts)

def edits2(word):

"All edits that are two edits away from `word`."

return (e2 for e1 in edits1(word) for e2 in edits1(e1))

import re

Suavizando Graficos de interpolacion lineal. Scipy en Python

 

Splines

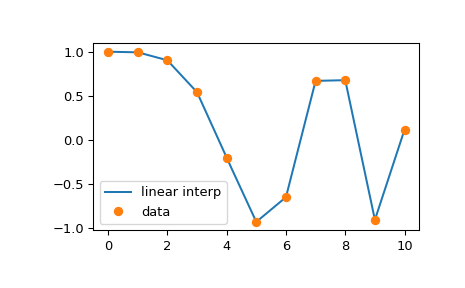
Por supuesto, la interpolación lineal por partes produce esquinas en los puntos de datos, donde se unen las piezas lineales. Para producir una curva más suave, puede utilizar cúbica splines, donde la curva de interpolación está hecha de piezas cúbicas con coincidencias primera y segunda derivada. En el código, estos objetos se representan mediante el CubicSpline instancias de clase. Una instancia se construye con el xy y matrices de datos, y luego se pueden evaluar utilizando el objetivo xnew valores: 

from scipy.interpolate import CubicSpline

spl = CubicSpline([1, 2, 3, 4, 5, 6], [1, 4, 8, 16, 25, 36])

spl(2.5)

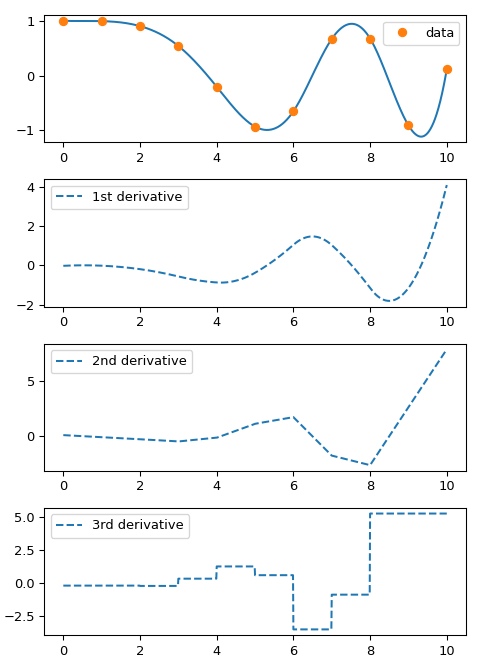
A CubicSpline objeto __call__ El método acepta tanto valores escalares como matrices. Acepta también un segundo argumento, nu, para evaluar la derivada de orden nu. Como ejemplo, trazamos las derivadas de un spline: 

from scipy.interpolate import CubicSpline

x = np.linspace(0, 10, num=11)

y = np.cos(-x**2 / 9.)

spl = CubicSpline(x, y)

import matplotlib.pyplot as plt
fig, ax = plt.subplots(4, 1, figsize=(5, 7))
xnew = np.linspace(0, 10, num=1001)
ax[0].plot(xnew, spl(xnew))
ax[0].plot(x, y, 'o', label='data')
ax[1].plot(xnew, spl(xnew, nu=1), '--', label='1st derivative')
ax[2].plot(xnew, spl(xnew, nu=2), '--', label='2nd derivative')
ax[3].plot(xnew, spl(xnew, nu=3), '--', label='3rd derivative')
for j in range(4):
    ax[j].legend(loc='best')
plt.tight_layout()
plt.show() 

 

 

Interpolaciòn lineal con Scipy en Python

 

Interpolación 1-D

Interpolación lineal.

Si todo lo que necesita es una interpolación lineal (también conocida como línea discontinua), puede usar el numpy.interp rutina. Se necesitan dos conjuntos de datos para interpolar, x, y y, y una tercera matriz, xnew, de puntos para evaluar la interpolación sobre: 

 

import numpy as np

x = np.linspace(0, 10, num=11)

y = np.cos(-x**2 / 9.0)

xnew = np.linspace(0, 10, num=1001)
ynew = np.interp(xnew, x, y)

import matplotlib.pyplot as plt
plt.plot(xnew, ynew, '-', label='linear interp')
plt.plot(x, y, 'o', label='data')
plt.legend(loc='best')
plt.show()

Guìa de usuario SciPy

 

Guía del usuario de SciPy

SciPy es una colección de algoritmos matemáticos y funciones de conveniencia creadas en NumPy . Agrega un poder significativo a Python al proporcionar al usuario Comandos y clases de alto nivel para manipular y visualizar datos.

Subpaquetes

SciPy está organizado en subpaquetes que cubren diferentes temas científicos. dominios informáticos. Estos se resumen en la siguiente tabla: 

Subpaquete	Descripción
cluster	Algoritmos de agrupamiento
constants	Constantes físicas y matemáticas.
fft	Transformadas discretas de Fourier
fftpack	Rutinas de transformación rápida de Fourier (heredadas)
integrate	Integración y solucionadores de ecuaciones diferenciales ordinarias.
interpolate	Interpolación y suavizado de splines.
io	Entrada y salida
linalg	Álgebra lineal
ndimage	Procesamiento de imágenes N-dimensionales
odr	Regresión de distancia ortogonal
optimize	Rutinas de optimización y búsqueda de raíces.
signal	Procesamiento de señales
sparse	Matrices dispersas y rutinas asociadas.
spatial	Algoritmos y estructuras de datos espaciales.
special	Funciones especiales
stats	Distribuciones y funciones estadísticas.

 

Introducciòn a la teorìa de confiabilidad

 

Introducción al campo de la ingeniería de confiabilidad 

La ingeniería de confiabilidad es un campo de estudio que se ocupa de la estimación, prevención y gestión de fallas combinando estadística, análisis de riesgos y física. Al comprender cómo pueden ocurrir o han ocurrido las fallas, podemos predecir mejor la vida útil de un producto o sistema, lo que nos permite administrar su ciclo de vida y los riesgos asociados con su falla. Todos los sistemas, componentes y estructuras de ingeniería eventualmente fallarán, y saber cómo y cuándo ocurrirá esa falla es de gran interés para los propietarios y operadores de esos sistemas. Debido a las similitudes entre el ciclo de vida de los sistemas de ingeniería y el ciclo de vida de los humanos, el campo de estudio conocido como análisis de supervivencia tiene muchos conceptos que se utilizan en la ingeniería de confiabilidad.

Todo el mundo es muy consciente de la importancia de la confiabilidad, especialmente cuando algo no funciona en el momento que esperamos. Ya sea que su automóvil no arranque, su televisor falle o la posibilidad de sufrir un retraso en la pista porque la unidad de aire acondicionado de su avión simplemente dejó de funcionar, sabemos que la falla del sistema es algo que todos queremos evitar. Cuando no se puede evitar, al menos queremos saber cuándo es probable que ocurra para poder realizar un mantenimiento preventivo antes de que surja la necesidad de un mantenimiento correctivo. La ingeniería de confiabilidad se utiliza con mayor frecuencia para sistemas que son de importancia crítica para la seguridad (como en la industria nuclear), o en sistemas que son numerosos (como vehículos o electrónica) donde el costo de los problemas de confiabilidad en toda la flota puede volverse muy costoso rápidamente.

Gran parte de la ingeniería de confiabilidad implica el análisis de datos (como los datos del tiempo hasta la falla) para descubrir los patrones de cómo ocurren las fallas. Una vez que entendemos cómo fallan las cosas, podemos usar esos patrones para pronosticar cómo ocurrirán las fallas a lo largo de la vida útil de una población de artículos, o la vida útil de uno o más artículos reparables. Esta biblioteca de Python está diseñada para ayudar con la parte del análisis de datos de la ingeniería de confiabilidad.

Primer ejemplo de confiabilidad en Python

 

Un ejemplo rápido 

En este ejemplo, crearemos una distribución Weibull y de esa distribución extraeremos 20 muestras aleatorias. Usando esas muestras ajustaremos una distribución Weibull de 2 parámetros. El proceso de ajuste genera la gráfica de probabilidad. Luego podemos acceder al objeto de distribución para trazar la función de supervivencia. 

En google Colab:

!pip install reliability

from reliability.Distributions import Weibull_Distribution
from reliability.Fitters import Fit_Weibull_2P
from reliability.Probability_plotting import plot_points
import matplotlib.pyplot as plt

dist = Weibull_Distribution(alpha=30, beta=2)  # creates the distribution object
data = dist.random_samples(20, seed=42)  # draws 20 samples from the distribution. Seeded for repeatability
plt.subplot(121)
fit = Fit_Weibull_2P(failures=data)  # fits a Weibull distribution to the data and generates the probability plot
plt.subplot(122)
fit.distribution.SF(label='fitted distribution')  # uses the distribution object from Fit_Weibull_2P and plots the survival function
dist.SF(label='original distribution', linestyle='--') # plots the survival function of the original distribution
plot_points(failures=data, func='SF')  # overlays the original data on the survival function
plt.legend()
plt.show()

Results from Fit_Weibull_2P (95% CI):
Analysis method: Maximum Likelihood Estimation (MLE)
Optimizer: TNC
Failures / Right censored: 20/0 (0% right censored) 

Parameter  Point Estimate  Standard Error  Lower CI  Upper CI
    Alpha         28.1696         3.57032   21.9733   36.1131
     Beta         1.86308         0.32449   1.32428   2.62111 

Goodness of fit    Value
 Log-likelihood -79.5482
           AICc  163.802
            BIC  165.088
             AD  0.83728 

 

Una característica clave de la confiabilidad es que las distribuciones de probabilidad se crean como objetos, y estos objetos tienen muchas propiedades (como la media) que se establecen una vez que se definen los parámetros de la distribución. El uso del operador de punto nos permite acceder a estas propiedades, así como a una gran cantidad de métodos (como extraer muestras aleatorias como se ve en el ejemplo anterior).

Cada distribución se puede visualizar en cinco gráficos diferentes. Estas son la función de densidad de probabilidad (PDF), la función de distribución acumulativa (CDF), la función de supervivencia (SF) [también conocida como función de confiabilidad], la función de riesgo (HF) y la función de riesgo acumulativo (CHF). Acceder a la trama de cualquiera de estos es tan fácil como cualquiera de los otros métodos. P.ej. dist.SF()en el ejemplo anterior es lo que traza la función de supervivencia utilizando el objeto de distribución que fue devuelto por el instalador.