3. Teoría y distribuciones de probabilidad
En
el corazón de predecir la confiabilidad está la comprensión de la
incertidumbre. La teoría de la probabilidad proporciona un marco para
cuantificar la incertidumbre y modelar eventos aleatorios, que es
esencial en el análisis de confiabilidad. Por ejemplo, ¿cuál es la
probabilidad de que un servidor falle en la siguiente hora? O, ¿qué tan
probable es que una caída de paquetes de red?
Conceptos básicos de probabilidad en confiabilidad
- Eventos aleatorios: en la confiabilidad, los eventos pueden ser falla de componentes , interrupción de la red , ocurrencia de errores , etc. La probabilidad asigna un número entre 0 y 1 para denotar qué probabilidad de ocurrir un evento (0 = nunca, 1 = cierto).
- Independencia: dos
eventos son independientes si la ocurrencia de uno no afecta la
probabilidad del otro. Por ejemplo, si dos servidores funcionan de forma
independiente, la falla de uno no cambia la probabilidad de falla del
otro.
- Probabilidad condicional: a
veces, los eventos no son independientes. La teoría de la probabilidad
explica esto a través de la probabilidad condicional, P (A | B): la
probabilidad de que se haya producido B dado que B ha ocurrido. En la
confiabilidad de la red, la probabilidad de una interrupción del
servicio podría aumentar dada una falla de energía en un centro de
datos.
Distribuciones de probabilidad comunes y sus aplicaciones
Diferentes distribuciones estadísticas modelo diferentes tipos de fenómenos aleatorios:
- Distribución normal: la
famosa "curva de campana". Definido por media (μ) y desviación estándar
(σ). Muchas métricas de rendimiento (como la latencia o el tiempo de
procesamiento) se aproximan a la normalidad en condiciones estables
debido al teorema del límite central. En la ciencia de datos, la
distribución normal a menudo se supone para errores o ruido.
- Distribución de Poisson: modela
el recuento de eventos en un intervalo fijo de tiempo o espacio, bajo
el supuesto de que los eventos ocurren independientemente a una
velocidad constante. Útil para contar eventos raros: por ejemplo, número
de fallas del servidor por mes o caídas de paquetes por hora. Si los
eventos ocurren con la velocidad λ (lambda), entonces el recuento
promedio en un intervalo es λ, y la varianza también es λ.
- Distribución exponencial: modela
el tiempo entre eventos independientes que ocurren a un ritmo constante
(es el análogo continuo de Poisson para los tiempos de llegada). A
menudo se usa para el tiempo de falso de los componentes que tienen una
tasa de falla constante. Tiene una propiedad sin memoria: la
probabilidad de sobrevivir otra hora no depende de cuánto tiempo ya esté
funcionando.
- Distribución log-normal: cuando
el logaritmo de una variable se distribuye normalmente, la variable se
distribuye logmalmente. Esto a menudo modela fenómenos donde los valores
se multiplican, como los tiempos de reparación o ciertas métricas
financieras. Los datos de confiabilidad que abarcan varios órdenes de
magnitud (por ejemplo, algunos componentes fallan en días, algunos en
años) podrían adaptarse a una distribución logarítmica normal.
- Distribución de Weibull: altamente
versátil y ampliamente utilizado en ingeniería de confiabilidad. Tiene
dos parámetros (forma β y escala η) que pueden modelar las tasas de
falla aumentando, constante o disminuyendo. Por ejemplo, un β <1
indica una tasa de falla decreciente (nuevos componentes-mortalidad
infantil), β = 1 corresponde a exponencial (fallas aleatorias) y β> 1
indica una tasa de falla creciente (fallas de desgaste). Weibull puede
responder: ¿Qué fracción de componentes sobreviven al tiempo T? y cuál
es la distribución de probabilidad de sus vidas.
Aplicaciones:
- Modelado de duraciones de tiempo de inactividad con exponenciales (si las fallas son aleatorias) frente a Weibull (si el desgaste es evidente).
- Modelado Número de errores o solicitudes con Poisson.
- Uso de distribución normal para la agregación de métricas de rendimiento.
Ejemplo de Python: demostremos algunas distribuciones usando scipy ( probability_distributions.py). Mostraremos cómo probar de un par de distribuciones y calcularemos las probabilidades:
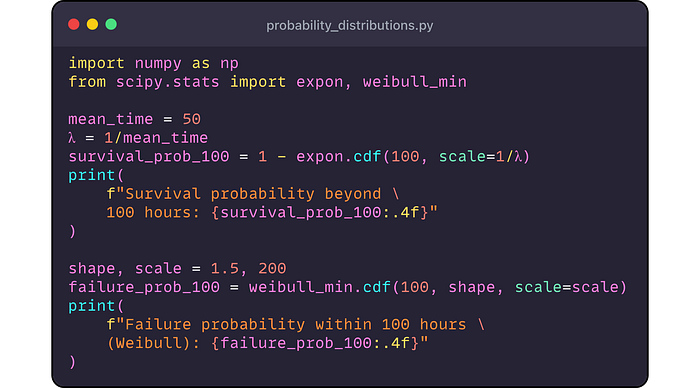
Producción:

Interpretación:
- Para
una distribución exponencial con 50 horas medias, hay una probabilidad
de ~ 13.5% que un componente sobrevive más allá de las 100 horas.
- Para
un Weibull (β = 1.5, η = 200h), hay un ~ 30.1% de posibilidades de que
el componente falle dentro de las primeras 100 horas.
Estas distribuciones ayudan a los ingenieros de confiabilidad a estimar la vida útil y los horarios de mantenimiento del plan.
4. Estadísticas inferenciales y pruebas de hipótesis
Si bien las estadísticas descriptivas describen los datos y las distribuciones de probabilidad modelo ,
las estadísticas inferenciales nos permiten hacer juicios sobre una
población basada en datos de muestra. Se trata de responder preguntas
como: "¿El nuevo sistema es más confiable que el anterior?" o "¿Existe una mejora del rendimiento, o estamos viendo fluctuación aleatoria?" .
Intervalos de confianza
Un intervalo de confianza (IC) da
un rango para un parámetro de población (como una media o proporción)
junto con un nivel de confianza (a menudo 95%). Por ejemplo, después de
observar una muestra de los tiempos de los servidores, podríamos decir: "Estamos 95% seguros de que el verdadero tiempo de actividad medio es entre 99.1% y 99.5%".
Puntos importantes:
- Un
IC del 95% no significa que haya una probabilidad del 95% de que la
media verdadera se encuentre en ese rango; Más bien, si repitiéramos el
experimento muchas veces, el 95% de esos IC contendrían la media
verdadera.
- Los intervalos más estrechos indican más precisión (a menudo debido a tamaños de muestra más grandes o menos variabilidad).
- En
confiabilidad, el IC se puede utilizar para las estimaciones de MTBF,
las tasas de falla, etc., para comunicar la incertidumbre.
Prueba de hipótesis
La prueba de hipótesis es un método formal para probar suposiciones (hipótesis) sobre un parámetro de población. Implica:
- Hipótesis nula (H0): la
suposición predeterminada (por ejemplo, "la nueva parte tiene la misma
tasa de falla que la parte anterior" o "sin diferencia en las medias").
- Hipótesis alternativa (H1): lo que sospecha que podría ser cierto (por ejemplo, "la nueva parte tiene una tasa de falla más baja").
- Estadística de prueba: un número calculado a partir de la muestra que, bajo H0, tiene una distribución conocida (como t, χ², etc.).
- Valor P: la
probabilidad de observar una estadística de prueba tan extrema como (o
más que) la de nuestra muestra, suponiendo que H0 sea cierta. Un pequeño
valor p (típicamente <0.05) conduce a rechazar H0 (evidencia de H1).
Pruebas paramétricas vs no paramétricas:
Las pruebas paramétricas asumen la distribución subyacente (a menudo
normal). Las pruebas no paramétricas no; Utilizan rangos u otros
enfoques, lo que los hace robustos para datos no normales.
Pruebas comunes:
- Tests t: para
comparar medios. Prueba t de una muestra (compare la media de muestra
con el valor conocido), prueba t de dos muestras (compare las medias de
dos grupos independientes), la prueba t emparejada (compare medias de
dos grupos relacionados, como antes/después en las mismas unidades).
- Prueba de chi-cuadrado (χ²): a
menudo utilizado para datos categóricos (por ejemplo, ¿los recuentos de
falla son independientes del día de la semana frente al fin de
semana?), O la bondad de ajuste (¿los datos siguen una distribución
dada?).
- ANOVA (análisis de varianza): generaliza
la prueba t para comparar medios en más de dos grupos (por ejemplo,
tiempos de falla en múltiples diseños). Prueba si al menos un grupo significa difiere.
- Prueba U de Mann-Whitney: una
alternativa no paramétrica a la prueba t de dos muestras para muestras
independientes. Compara medianas utilizando sumas de rango, utilizadas
cuando los datos no se distribuyen normalmente.
- Prueba de rango firmado de Wilcoxon: no paramétrico para datos emparejados (alternativa a la prueba t pareada).
- Mann-Whitney U vs T-Test: Mann-Whitney
no asume normalidad y se basa en rangos. Es útil en confiabilidad al
comparar, digamos, duraciones de tiempo de inactividad de dos sistemas
que están muy sesgados.
Ejemplo de Python: Supongamos
que queremos probar si un nuevo hardware de servidor tiene un tiempo de
respuesta medio diferente al de hardware anterior. Recolectamos dos
muestras de tiempos de respuesta. Usamos una prueba t de dos muestras si
los datos son más o menos normales, o Mann-Whitney U si no ( hypothesis_testing.py).
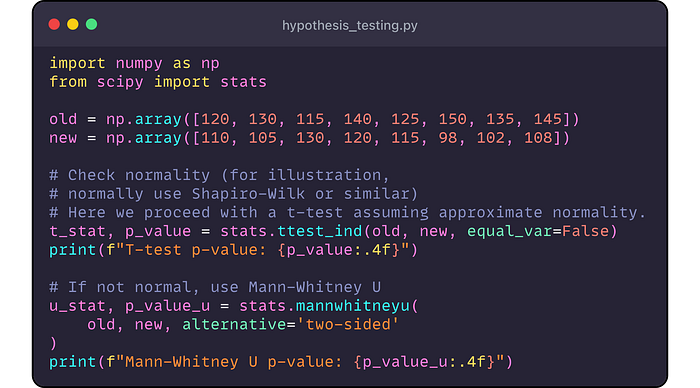
Producción:

En
ambas pruebas, P ≈ 0.03, que es inferior a 0.05. Rechazaríamos la
hipótesis nula y concluyeron los tiempos de respuesta del nuevo hardware
difieren significativamente de los viejos hardware. Observar los datos,
probablemente el nuevo hardware es más rápido (tiempos más bajos).
(Nota:
siempre verifique los supuestos. Si las variaciones difieren, use la
prueba t de Welch (como lo hicimos). Si los datos no son normales,
confíe en Mann-Whitney u transforma los datos).
Interpretación y uso en confiabilidad:
Las pruebas de hipótesis en confiabilidad podrían ayudar a responder:
- "¿Una
actualización de software mejora el tiempo medio entre fallas (MTBF)?"
(Compare MTBF antes y después a través de la prueba t o la prueba no
paramétrica).
- "¿La
tasa de falla es la misma en diferentes temperaturas operativas?"
(Prueba de chi-cuadrado para recuentos o ANOVA para medios).
- "¿Un nuevo proceso produce una mayor vida media del producto?" (Mann-Whitney U para datos de por vida).
Recuerde,
la significación estadística no es la misma que la importancia
práctica. Especialmente en ingeniería, una mejora estadísticamente
detectable podría ser muy pequeña en magnitud: siempre considere el
tamaño del efecto y los intervalos de confianza.
5. Análisis de regresión y modelado predictivo
A menudo, queremos predecir una cantidad de los demás o comprender las relaciones entre las variables. El análisis de regresión es el caballo de batalla aquí.
Regresión lineal (y regresión lineal múltiple)
La
regresión lineal modela la relación entre una o más variables
independientes (x) y una variable dependiente continua (y) ajustando una
ecuación lineal:
Y = β0+β1 x1+β2 x2+...+βn xn+ϵ
donde los β son coeficientes a aprender, y ε es el término de error.
- Regresión lineal simple: una x, una Y. Por ejemplo, predice el tiempo de falla (y) a partir de la temperatura de funcionamiento (x).
- Regresión múltiple: múltiples
X (por ejemplo, predecir la carga del servidor a partir del recuento de
usuarios, la tasa de solicitud y la relación de accesorios de caché).
Salidas clave:
- Coeficientes (β): indique
el tamaño del efecto de cada predictor. Por ejemplo, β1 = -2 horas/° C
podría significar que cada aumento de grado en la temperatura reduce el
tiempo de falla en 2 horas en promedio.
- Intercept (β0): el y predicho cuando todo x = 0 (a veces no es significativo dependiendo del contexto).
- R-cuadrado (r²): proporción
de varianza en y explicada por X's. R² = 0.8 significa que el 80% de la
variabilidad en el tiempo de falla se explica por el modelo (y el 20%
no está explicada). Es una medida de bondad de ajuste.
- R² ajustado: como R² pero penaliza la adición de predictores irrelevantes (para desalentar el sobreajuste).
- Valores p para coeficientes: prueba
si cada β es significativamente diferente de cero (hipótesis nula: β =
0). El bajo valor P significa que el predictor probablemente tiene un
impacto real en Y.
- Residuos: las
diferencias entre Y. Analizar residuos ayudan a verificar si los
supuestos del modelo lineal se mantienen (varianza constante, sin
patrones, normalidad de errores).
Para fiabilidad y rendimiento:
- Use
la regresión para identificar cuellos de botella (por ejemplo, ¿qué tan
fuertemente aumenta la latencia con la carga del usuario?).
- Predecir el tiempo a la siguiente falla basada en las condiciones de uso.
- Modelo de consumo de energía versus rendimiento.
Regresión logística
Cuando
el resultado es binario (éxito/falla, arriba/abajo, aprobación/fallas),
la regresión logística modela la probabilidad del evento (a menudo
codificada como 1) utilizando una función logística. Emite coeficientes
que se pueden interpretar en términos de odds ratios. En confiabilidad,
la regresión logística podría modelar la probabilidad de falla dentro de
un período dadas características como temperatura, carga o proveedor.
Ejemplo: regresión lineal en Python
Supongamos
que sospechamos que el tiempo de inactividad mensual de un servidor (Y,
en horas) está relacionado con la temperatura promedio de la CPU (x, en
° C) y la edad del servidor (x₂, en años). Recopilamos datos y
ejecutamos una regresión ( regression_analysis.py):
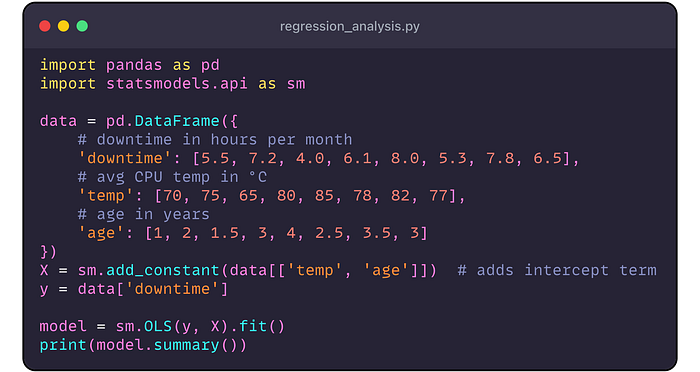
Salida (resumida):
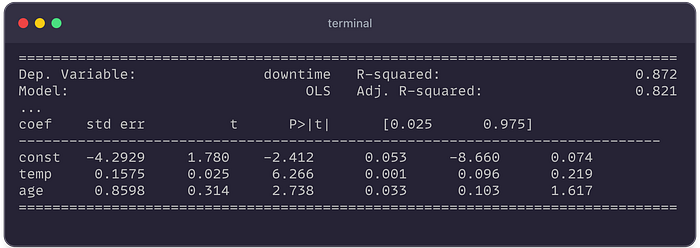
Control de llave:
- R² ≈ 0.872: El modelo explica ~ 87.2% de la varianza de tiempo de inactividad, bastante alta.
- Coeficiente para
temp
es ~ 0.1575 (p ≈ 0.001, muy significativo). Esto sugiere que cada
temperatura adicional de 1 ° C está asociada con ~ 0.158 horas de
inactividad adicionales por mes, manteniendo constante la edad. - Coeficiente para
age
es ~ 0.8598 (p ≈ 0.033). Cada año adicional de edad del servidor agrega
~ 0.86 horas de tiempo de inactividad por mes, en promedio. - La
intersección (const) es de aproximadamente -4.29 (P ~ 0.053, límite).
Interpretándolo: si temp = 0 (no es físicamente significativo aquí) y
edad = 0, el tiempo de inactividad sería -4.29 (lo que indica que el
modelo podría no ser válido fuera del rango de datos; generalmente nos
importa más los βs para los predictores).
Validaríamos
este modelo verificando las gráficas residuales (no aseguraremos
patrones obvios o heteroscedasticidad) y tal vez usándolo para predecir
el tiempo de inactividad para la planificación del mantenimiento.
El análisis de regresión se extiende aún más:
- Regresión polinomial para relaciones no lineales (o transformaciones de uso).
- Regularización (Ridge, Lasso) para manejar la multicolinealidad o evitar el sobreajuste en datos de alta dimensión.
- Diagnóstico: por ejemplo, use la distancia de Cook para detectar si un atípico influye indebidamente en el modelo.
En
ingeniería de confiabilidad, la regresión puede integrarse con el
análisis de falla: predecir las tasas de falla de los factores de
estrés, los recuentos de reclamos de garantía modelo a lo largo del
tiempo, etc.
6. Análisis y pronóstico de series de tiempo
Muchos
datos de confiabilidad y rendimiento se recopilan con el tiempo: piense
en los recuentos diarios de errores del sistema, minutos semanales de
tiempo de inactividad o lecturas de sensores del equipo. El análisis de
la serie temporal se ocupa de dichos datos, teniendo en cuenta el orden
temporal, que introduce patrones únicos como tendencias, estacionalidad y
autocorrelación.
Conceptos clave en series de tiempo
- Statarity: una
serie temporal estacionaria tiene una media, varianza y estructura de
autocorrelación constante con el tiempo. La estacionariedad es a menudo
un requisito para muchos métodos de pronóstico estadístico. Si los datos
no son estacionarios (por ejemplo, tienen una tendencia o un patrón
estacional), a menudo los transformamos (a través de la diferencia, el
ritmo, etc.) a la estacionariedad.
- Tendencia: aumento
o disminución a largo plazo en los datos. Ejemplo: la mejora gradual de
la latencia de la red durante años debido a un mejor hardware.
- Estacionalidad: patrón
regular que se repite (diariamente, semanalmente, anualmente). Ejemplo:
picos de tráfico todos los días de la semana a las 9 a.m.
- Ruido (residual): fluctuación aleatoria que no se explica por tendencia o estacionalidad.
La
verificación de la estacionaridad se puede hacer trazando (una serie
"plana" indica estacionaridad) o pruebas estadísticas como la prueba de
Dickey-Fuller (ADF) aumentada.
Técnicas de pronóstico
ARIMA (promedio móvil integrado autorregresivo): una
poderosa clase de modelos para pronosticar series de tiempo
estacionarias (y ARIMA puede manejar series no estacionarias por la
parte "integrada").
- AR (P): parte autorregresiva: regresión en valores rezagados (pasados).
- I (D): Integrado: orden de diferenciación para eliminar las tendencias (d = número de diferencias).
- MA (Q): parte
móvil del promedio: regresión en errores de pronóstico rezagados. Una
ARIMA simple podría ser ARIMA (1,1,0): utiliza un retraso de la serie,
una diferencia para garantizar la estacionariedad y no hay términos de
promedio móvil. Los modelos ARIMA pueden capturar patrones como si el
tiempo de inactividad de hoy está relacionado con el tiempo de
inactividad de ayer (AR) o si hay algún efecto de choque que se disipa
(MA). La Arima estacional (Sarima) agrega términos estacionales para
manejar patrones como la estacionalidad semanal.
Alisado exponencial (ETS): estos
métodos (p. Ej., Las ganancias de HOLT) están más en la familia
ajustada a la curva. Pese más observaciones recientes (con pesos
exponencialmente disminuidos para observaciones más antiguas). Hay
variaciones:
- Suavizado exponencial simple (solo para nivel, sin tendencia).
- Lineal de Holt (agrega tendencia).
- Holt-Winters (agrega tendencia y estacionalidad; puede ser estacionalidad aditiva o multiplicativa).
El suavizado exponencial es intuitivo: el pasado reciente es más relevante para el futuro cercano . A menudo es efectivo para pronósticos a corto plazo y es computacionalmente ligero.
Otros métodos avanzados: Profeta
(por Facebook, para pronósticos automatizados rápidos con
estacionalidad/efectos de vacaciones), modelos de espacio de estado o
enfoques de aprendizaje automático como redes LSTM para patrones
complejos.
Ejemplo de Python: pronóstico de ARIMA
Usemos una ARIMA simple para pronosticar algo como la falla mensual cuenta para un sistema ( time_series_forecasting.py). Simularemos una pequeña serie de tiempo y pronosticaremos:
Producción:

Esto
indica que el modelo pronostica alrededor de 19 fallas en el próximo
mes, y ~ 20 en el mes posterior. (Nuestros datos originales terminaron a
las 18, por lo que está extrapolando la tendencia ascendente).
Para un escenario real, usaría gráficos ACF/PACF o Auto_arima (desde pmdarima Biblioteca) para elegir P, D, Q, Q e incluir términos estacionales si es necesario.
Casos de uso en confiabilidad y rendimiento:
- Previsión de fallas: predecir
los recuentos de fallas o tiempos futuros para programar el
mantenimiento. Por ejemplo, pronostice cuándo la probabilidad de que
falle una matriz de disco exceda un umbral.
- Planificación de capacidad: use
series temporales de uso de recursos (CPU, memoria, red) para
pronosticar cuándo los sistemas alcanzarán la capacidad, activando la
escala o las actualizaciones.
- Detección de anomalías: identifique
las desviaciones del pronóstico o el rango esperado como anomalías (si
lo real está lejos de los intervalos de confianza de la confianza).
El
análisis de la serie temporal respeta la estructura temporal de los
datos, haciendo que los pronósticos y la detección de anomalías sean más
precisos que los enfoques que ignoran las dependencias del tiempo.
7. Análisis de fiabilidad y supervivencia
La
ingeniería de confiabilidad a menudo trata los datos de tiempo de
evento (como el tiempo de falla, el tiempo entre errores). El análisis
de supervivencia es el campo estadístico que aborda exactamente eso, con
raíces en estadísticas médicas (tiempos de supervivencia del paciente)
pero igualmente aplicable a la ingeniería (vida útil del componente).
Estimador de Kaplan-Meier (función de supervivencia)
El
estimador de Kaplan-Meier (KM) es una estadística no paramétrica
utilizada para estimar la función de supervivencia S (t): la
probabilidad de que el tiempo hasta el evento sea mayor que t (es decir,
el elemento sobrevive más allá del tiempo t). Es útil cuando ha
"censurado" los datos (por ejemplo, si una prueba terminó antes de que
algunas unidades fallaran, esas unidades están censuradas a la derecha).
El
método KM esencialmente multiplica las probabilidades de sobrevivir
cada intervalo de tiempo donde ocurren los eventos. A menudo se
visualiza como una curva de supervivencia gradual, donde cada gota
corresponde a un evento (falla). Por ejemplo, KM puede decirle "Después
de 1000 horas, el 90% de los dispositivos aún funcionan".
Análisis de Weibull
Presentamos
la distribución de Weibull antes. El análisis de Weibull implica
ajustar una distribución de Weibull a los datos de falla. Una gráfica de
Weibull (o utilizando la estimación de máxima verosimilitud) puede
estimar los parámetros de forma (β) y escala (η):
- A
partir de estos, puede calcular métricas como la confiabilidad en el
tiempo t (que es s (t) para Weibull), la tasa de falla en función del
tiempo, etc.
- Por
ejemplo, la función de peligro (tasa de falla instantánea en el tiempo
t) para Weibull puede aumentar, disminuir o mantenerse constante
dependiendo de β. Si β> 1, el peligro aumenta con el tiempo
(envejecimiento/desgaste); Si β <1, el peligro disminuye (dominan las
fallas tempranas); β = 1 da un peligro constante (fallas independientes
aleatorias, igual que exponencial).
Tiempo
medio entre fallas (MTBF): a menudo se usa como una métrica de
confiabilidad, es básicamente la media de la distribución del tiempo de
falla (para sistemas reparables). Para exponencial, mtbf = 1/λ (la
media). Para Weibull, MTBF = η * γ (1 + 1/β) (si β> 1). Tenga cuidado: MTBF
es el tiempo promedio entre fallas en operación continua y supone que
después de una falla se repara el artículo y vuelve a poner en servicio;
A menudo se usa indistintamente con MTTF (tiempo medio de falla) para
sistemas no reparables.
Análisis de supervivencia en Python
pitón lifelines
La biblioteca es excelente para el análisis de supervivencia, pero
incluso sin ella, podemos hacer lo básico. Ilustramos Kaplan-Meier
usando líneas de vida ( survival_analysis.py):
(Este
código generaría probabilidades de supervivencia a 100 h, 250h, 450h.
Si bien no podemos trazar aquí, generalmente usaríamos kmf.plot_survival_function() para ver la curva.)
Salidas:

Esto
podría indicar que todos los componentes sobreviven más allá de las 100
h, en 250 h de aproximadamente el 67% sobreviven, y en 450h
aproximadamente 33% sobreviven.
Ejemplo de análisis de Weibull: Uso de Scipy para adaptarse a un Weibull o usar líneas de vida ' WeibullFitter también es posible. Por brevedad:
- Si encajamos en un Weibull y obtenemos β ≈ 1.5, η ≈ 320h, podemos informarlos.
- Confiabilidad a 200h = exp [-(200/h)^b].
- MTBF (si estos fueran reparables) podría calcularse a partir de β, η.
Función de peligro y mtbf
La función de peligro H
(t) es la tasa de falla en el momento t, dada la supervivencia hasta t.
Para exponencial, h (t) = constante (λ). Para Weibull, h (t) = βη (t/η)
β-1H (t) = \ frac {\ beta} {\ eta} (t/\ eta)^{\ beta-1} h (t) = ηβ
(t/η) β-1. Si β = 2, eso es lineal en T (aumento de riesgo). Si β <1,
el peligro disminuye con el tiempo.
MTBF,
como se mencionó, a menudo se usa como resumen. Por ejemplo, si un
sistema tiene un MTBF de 1,000 horas y MTTR (tiempo medio de reparación)
de 10 horas, se puede calcular la disponibilidad (dado un proceso de
estado estable) como MTBF/(MTBF+MTTR).
Las
técnicas de análisis de supervivencia aseguran que tengamos en cuenta
la censura y caracterizemos adecuadamente los datos de la vida. Son
fundamentales en industrias como aeroespacial, fabricación e
infraestructura en la nube para evaluaciones de confiabilidad.
8. Control de procesos estadísticos y detección de anomalías
Asegurar la confiabilidad y el rendimiento continuos no se trata solo de un análisis único, requiere un monitoreo continuo. El control de procesos estadísticos (SPC) proporciona
herramientas (especialmente cuadros de control) para monitorear los
procesos en tiempo real, distinguiendo la variación normal de las
anomalías.
Gráficos de control (SPC)
Originario
del control de calidad de fabricación, los gráficos de control trazan
una estadística con el tiempo con una línea central (promedio) y límites
de control (a menudo ± 3σ para el proceso, o basados en percentiles).
Tipos comunes:
- X̄ (X-BAR) y R (rango) o S (STD Dev) gráficos: para datos continuos donde tiene subgrupos. X̄ monitorea la media de los subgrupos, R/S monitorea la variabilidad.
- Individuos (i) y cuadros de rango móvil (MR): para
observaciones individuales (sin subgrupos), típicos en el monitoreo de
algo como los minutos diarios de tiempo de inactividad. El cuadro i
monitorea el punto de datos, el Sr. monitorea la variabilidad a corto
plazo.
- Chart P, C-Chart, etc.: Para datos de atributos (como la fracción defectuosa, recuento de defectos por unidad).
La idea es detectar la variación de causa especial (señales) en medio de la variación de causa común (aleatoriedad
natural). Si un punto cae fuera de los límites de control o exhibe
ciertos patrones (como 8 puntos seguidos por encima de la media),
sugiere una anomalía que debe investigarse. Para la confiabilidad de la
red, una tabla de control podría monitorear las tasas de error; Un pico
repentino más allá de los límites indica un incidente.
Técnicas de detección de anomalías (atípicos)
Más
allá de SPC, especialmente en contextos de ciencia de datos, una
variedad de métodos detectan valores atípicos o anomalías en los datos:
- Método de puntaje Z: calcule
cuántas desviaciones estándar de distancia es un punto de la media. Una
regla común es | Z | > 3 es un valor atípico (para datos normales).
En un sistema en vivo, uno podría calcular la media rodante y la ETS
para calcular una puntuación Z en tiempo real para nuevas observaciones.
- Método IQR: use el rango intercuartil. Cualquier punto por debajo de Q1–1.5 IQR o por encima de Q3 + 1.5 IQR está marcado. Esto es robusto para las distribuciones no normales y a menudo se visualiza a través de diagramas de caja.
- Bosque de aislamiento: un
enfoque de aprendizaje automático que construye un conjunto de árboles
para aislar observaciones. Los atípicos, siendo más fáciles de aislar,
terminan con caminos más cortos en el conjunto de árboles. Es efectivo
para datos de alta dimensión y puede manejar grandes conjuntos de datos.
- Factor atípico local (LOF): analiza
la densidad local. Los puntos en regiones de baja densidad en
comparación con sus vecinos son valores atípicos. Útil cuando los datos
tienen grupos.
- SVM de una clase: entrena un modelo en datos "normales" para clasificar si nuevos puntos pertenecen a esa distribución o no.
- Pruebas estadísticas para valores atípicos: hay
pruebas como la prueba de Grubbs, pero las asumen distribuciones
subyacentes y son menos comunes en los datos a gran escala.
En monitoreo de confiabilidad:
- La detección de anomalías puede
atrapar a una máquina que se comporta de manera extraña antes de que
falle (lecturas de vibración fuera del rango normal, por ejemplo).
- Operaciones de SPC en TI: Tiempos
de respuesta de seguimiento o rendimiento de consulta; Los gráficos de
control pueden alertar si el rendimiento se degrada más allá de la
variación normal.
Ejemplo de Python: detectemos valores atípicos en un conjunto de datos de mediciones de latencia utilizando Z-Score e IQR ( anomaly_detection.py):
Producción:

Ambos métodos marcan 400 y 500 ms
como valores atípicos, lo que tiene sentido en este conjunto
principalmente alrededor de ~ 20 ms. En la práctica, uno podría preferir
IQR para distribuciones sesgadas o usar estadísticas robustas (mediana,
loca), mientras que Z-Score está bien si los datos son más o menos
normales.
9. Estadísticas bayesianas y sus aplicaciones
Hasta
ahora, muchos métodos que discutimos están enraizados en estadísticas
frecuentistas (parámetros fijos, probabilidad de frecuencia a largo
plazo). Las estadísticas bayesianas ofrecen una perspectiva diferente:
trata los parámetros como variables aleatorias con distribuciones
previas y actualiza esas creencias con datos (a través del teorema de
Bayes) para obtener distribuciones posteriores.
Inferencia bayesiana vs frecuentista
- Inferencia bayesiana: comienza
con una creencia previa sobre un parámetro (por ejemplo, la tasa de
falla de un nuevo componente es de alrededor del 1% por 1000 horas, pero
no está seguro). A medida que recopila datos, el teorema de Bayes
actualiza esta creencia. El resultado es una distribución posterior para
el parámetro, que puede resumir (intervalo medio, creíble) para la toma
de decisiones.
- Intervalos creíbles frente a intervalos de confianza: un intervalo creíble del 95% significa que
hay un 95% de probabilidad de que el parámetro verdadero se encuentre
en ese intervalo (dados los datos y anteriores). Esta es una
interpretación más intuitiva, al costo que tenía que especificar un
anterior.
- Bayesiano vs frecuentista en la práctica: con
grandes datos, los resultados a menudo convergen. Las diferencias se
muestran con datos limitados o cuando se incorpora conocimiento previo
es valioso. Por ejemplo, en confiabilidad, si sospechamos firmemente que un
nuevo diseño es mejor debido a las ideas de ingeniería, un enfoque
bayesiano puede incluir formalmente esa sospecha como anterior, mientras
que el enfoque frecuentista trataría los datos sin ese contexto.
Redes bayesianas y razonamiento probabilístico
Una
red bayesiana (BN) es un modelo gráfico (gráfico acíclico dirigido)
donde los nodos son variables aleatorias y bordes codifican dependencias
condicionales. Es como un mapa de relaciones probabilísticas. Los BN
son útiles en confiabilidad para modelar sistemas complejos:
- Los nodos podrían representar estados de componentes (trabajo/fallido) o condiciones del sistema.
- Los
bordes representan influencia (por ejemplo, una falla de suministro de
alimentación aumenta la posibilidad de falla del servidor).
- Una
vez construido, puede hacer inferencia probabilística: evidencia dada
(como un sensor que lee a alta temperatura), ¿cuál es la probabilidad de
que el sistema falle en una hora?
Las
redes bayesianas permiten una actualización de confiabilidad casi en
tiempo real a medida que entra evidencia. Por ejemplo, en un centro de
datos, un BN podría combinar evidencia de sensores de temperatura,
velocidades de ventilador y eventos de aceleración de CPU para
actualizar la probabilidad de una falla inminente del servidor.
Ejemplo: Inferencia bayesiana en Python
Usaremos PYMC3 (una biblioteca de modelado bayesiano) para ilustrar un análisis bayesiano simple ( bayesian_analysis.py).
Supongamos que queremos estimar la probabilidad P de que un servidor
sobrevivirá a una prueba de estrés, basada en la prueba de Servidores y
los éxitos K. Tenemos una creencia previa (por ejemplo, Beta Prior) y
actualizamos con datos.
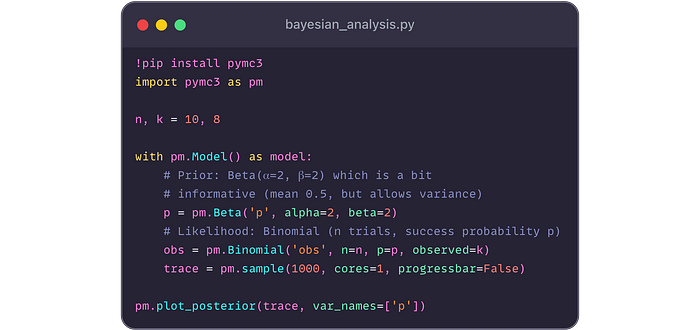
(Asumimos que la biblioteca y la trama funcionarían; en forma de texto, describiríamos el resultado).
El
resultado sería una distribución posterior para P (probabilidad de
supervivencia del servidor). Con 8/10 observados, el posterior podría
alcanzar alrededor de 0.8. El beta (2,2) anterior (que es como observar 1
éxito adicional y 1 falla previa a los datos) lo cambiaría ligeramente.
El pm.plot_posterior Mostraría una distribución, tal vez algo así como un intervalo creíble del 95% [0.55, 0.95] y media ~ 0.78.
Ideas bayesianas clave:
- Si
tuviéramos solo 2 pruebas con 2 éxitos, un frecuentista podría dar una
estimación de punto P̂ = 1 (y un CI). Un bayesiano con un anterior
sensato produciría un centrado posterior más bajo (porque con n = 2, ver
2 éxitos no nos convence absolutamente de que P está cerca de 1, podría
ser suerte).
- En
confiabilidad, los métodos bayesianos pueden combinar datos de campo y
la opinión de expertos. Si los datos históricos sugieren una tasa de
fracaso, pero los expertos creen que un nuevo diseño reduce las fallas a
la mitad, un anterior puede codificar la creencia experta y los datos
lo actualizarán.
- Los
intervalos creíbles bayesianos pueden ser más sencillos para
interpretar para los tomadores de decisiones ("Hay una probabilidad del
95% de que la tasa de falla sea entre x e y por hora").
Las
estadísticas bayesianas también se extienden a modelos avanzados:
modelos jerárquicos (para datos de confiabilidad de nivel múltiple), la
regresión bayesiana (con coeficientes posteriores), etc. Con la
computación moderna, métodos como MCMC (cadena de Markov Monte Carlo)
hacen que el análisis bayesiano sea más accesible.
10. Estudios de casos del mundo real
Vamos
a unirlo todo con algunos escenarios que demuestren cómo estas
herramientas estadísticas se pueden aplicar en la práctica:
Estudio de caso 1: Diagnóstico de cuellos de botella de rendimiento de la red
Escenario: el
sistema distribuido de una empresa experimenta desaceleraciones
intermitentes. Los ingenieros de confiabilidad recopilan métricas: uso
de CPU, uso de memoria, E/S de red y tiempos de respuesta en 50
microservicios durante 12 meses.
Acercarse:
- Análisis descriptivo: Primero,
resume los tiempos de respuesta por servicio (media, percentil 95,
etc.). Visualice con gráficos de caja para ver qué servicios tienen una
mayor variabilidad (posibles cuellos de botella).
- Análisis de regresión: construya
un modelo de regresión múltiple para el tiempo de respuesta con
predictores como CPU, memoria, E/S de red. Supongamos que el Servicio A
muestra el tiempo de respuesta aumenta fuertemente con el uso de la CPU
(β_CPU High, P <0.01) y la E/S de red (P <0.05), pero no la
memoria. Esto apunta a la saturación de la CPU y la congestión de la red
como los principales culpables.
- Serie de tiempo: analizar
la serie temporal de tiempos de respuesta. Realice una descomposición
estacional, tal vez encuentre un patrón diario (más lento a las 2 a.m.
cuando funcionan las copias de seguridad). Use ARIMA para modelar el
comportamiento de referencia por servicio. Anomalías de la bandera donde
la latencia real excede 3σ de predicción.
- Detección de anomalías: implementa
la detección de anomalías en tiempo real (por ejemplo, un bosque de
aislamiento en métricas recientes) para atrapar las desaceleraciones
futuras temprano, desencadenando alertas.
- Resultado: identificaron
que ciertos trabajos cron causaron picos de CPU (variación de causa
especial). Al tambaleando esos trabajos, el rendimiento se estabilizó.
Los gráficos de SPC en curso para la latencia de cada servicio ayudan a
garantizar que se mantenga así.
Estudio de caso 2: Fallas de pronóstico en la infraestructura de la nube utilizando Weibull
Escenario: un
proveedor de almacenamiento en la nube quiere predecir fallas en la
unidad de disco para reemplazar las unidades preventivamente. Tienen
datos de falla histórica de miles de unidades.
Acercarse:
- Ajuste de distribución: usan
el análisis Weibull en las vidas de la unidad. El ajuste revela β ≈ 1.2
(una tasa de falla ligeramente aumentada, insinúa el desgaste) y η ≈ 5
años (vida característica donde ~ 63.2% han fallado).
- Análisis de supervivencia: las
curvas de Kaplan-Meier se trazan para unidades de diferentes modelos o
patrones de uso. Un modelo muestra fallas de vida temprana
significativamente más altas (mortalidad infantil, β <1
inicialmente).
- Planificación: utilizando
el modelo Weibull, pronostican cuántas unidades probablemente fallarán
en el próximo trimestre (integrando la tasa de falla con el tiempo o
simulando). Esto ayuda a garantizar suficientes repuestos y
mantenimiento del horario.
- Intervalos de confianza: proporcionan a la gerencia un intervalo de confianza del 90% para el número de fallas (para dar cuenta de la incertidumbre).
- Resultado: el
proveedor implementó una política para reemplazar las unidades de
manera proactiva a los 4 años de servicio (cuando la curva de
supervivencia cae por debajo de un umbral). Esto redujo el tiempo de
inactividad inesperado en un 30%.
Estudio de caso 3: detección de anomalías en tiempo real en sistemas a gran escala
Escenario: una
empresa FinTech procesa millones de transacciones diariamente. La
fiabilidad es primordial. Instrumentan todo: tasas de transacción,
recuentos de errores, latencias, uso de memoria, etc., en cientos de
servidores.
Acercarse:
- Control estadístico del proceso: para
cada métrica (por servidor o agregado), mantienen cuadros de control.
Por ejemplo, una tasa de error de un grado P monitorea por 1000
transacciones. Si la tasa de error excede los límites de control, se
desencadena la respuesta al incidente.
- Detección atípica: usan un bosque de aislamiento en
una ventana rodante de datos multivariados (que combinan varias
métricas) para atrapar patrones inusuales que podrían indicar un ataque o
error (por ejemplo, fuga de memoria que causa la degradación gradual
del rendimiento).
- Razonamiento bayesiano: emplean
una red bayesiana para el diagnóstico de fallas. Por ejemplo, si el
tiempo de respuesta del servicio es alto y la CPU es bajo, pero la
memoria es alta, el BN infiere una fuga de memoria con alta
probabilidad, guiando a los ingenieros a la causa raíz más rápido.
- Acciones automatizadas: cuando
se detectan anomalías con alta confianza (p. Ej., Z-Score >> 3 en
latencia), los scripts automatizados giran instancias adicionales del
servidor o reinician servicios para evitar fallas.
- Resultado: la
combinación de gráficos de control para la variación esperada y la
detección avanzada de valores atípicos para temas novedosos proporciona
una red robusta. Logran la disponibilidad de "cinco nueves" (99.999%)
porque la mayoría de los problemas se capturan y mitigan en segundos o
minutos.
Resumen
Desde
calcular una media simple hasta interpretar una curva de supervivencia o
ajustar un modelo bayesiano, las estadísticas es la base que permite a
los ingenieros de confiabilidad y a los científicos de datos transformar
los datos sin procesar en ideas procesables. Al colocar progresivamente
estas técnicas (estadísticas descriptivas para la comprensión, la
probabilidad de modelar la incertidumbre, las estadísticas inferenciales
para la toma de decisiones, la regresión y las series de tiempo para la
predicción y los métodos avanzados para ideas profundas), puede abordar
complejos desafíos del mundo real en la confiabilidad de la red, el
pronóstico de fallas y la optimización del rendimiento. Recuerde siempre
combinar el rigor estadístico con el contexto de ingeniería: las
estadísticas nos dicen lo que dicen los datos, la sabiduría de
ingeniería nos dice por qué y cómo actuar en consecuencia.