Uso de Python para resolver uno de los problemas más comunes en ingeniería
Creación de un marco genérico para el análisis de puntos operativos
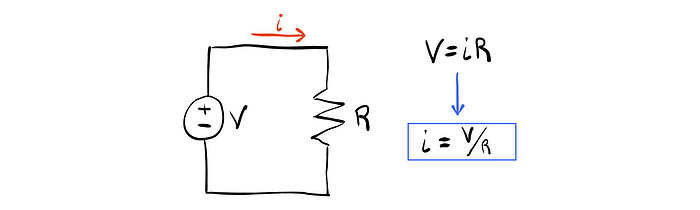
Simple, ¿verdad? Desafortunadamente, la mayoría de los problemas del mundo real nunca son tan fáciles. Por ejemplo, ¿qué pasaría si le dijera que a medida que la resistencia se calienta, su valor de resistencia cambia, esencialmente lo que hace que la resistencia sea una función de la corriente? Terminamos con una ecuación de la siguiente forma:
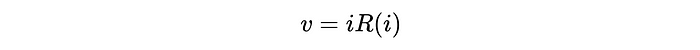
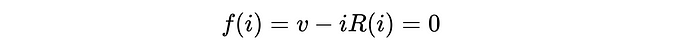
Al hacer esto, hemos vuelto a surgir nuestro problema. En lugar de resolver la corriente directamente en términos de todas las demás variables, podemos intentar encontrar el valor de la corriente que se puede ingresar en el lado izquierdo de la ecuación para que se evalúe en cero. ¿Por qué formulamos el problema como este? ¡Porque existen un montón de algoritmos numéricos que existen (método de bisección, método de Newton, etc.) para resolver este tipo exacto de problema! Y a la mayoría de los algoritmos no les importa cuán complicado sea el lado izquierdo de la ecuación: ni siquiera tiene que tener una forma algebraica cerrada (es decir, podría estar compuesta de datos discretos interpolados, integrales evaluadas numéricamente o literalmente ningún tipo de función de complejidad arbitraria para evaluar). Siempre que podamos plantear nuestro problema en forma de F (x) = 0, (casi) siempre podemos encontrar una solución al problema (y el código puede modificarse/extenderse fácilmente si la declaración del problema cambia, no es necesario volver a hacer álgebra).
El resto de este artículo va a recorrer un ejemplo de cómo aplicar la metodología de búsqueda de raíces a un problema un poco más complicado y del mundo real, con énfasis en las técnicas de estructuración y organización de código de sonido en Python. Aunque el problema (que determina la velocidad de flujo del agua en un sistema de tubería/bomba) es algo específico de dominio, la metodología y las técnicas de codificación que se utilizan son completamente generales y aplicables a todos los dominios de ingeniería. Con esto en mente, intentaré mantener los aspectos de modelado físico del problema a un alto nivel, de modo que, independientemente de los antecedentes técnicos, los objetivos de aprendizaje principales del artículo aún se presentan claramente.
Como nota al margen, mi "especialidad" de dominio en estos días se encuentra en el ámbito de los controles de motor y la electrónica de alimentación, y estoy muy lejos de las aplicaciones de bombeo/tuberías. No he tocado el tema en años, pero pensé que sería un ejemplo interesante del tema en cuestión. Estoy seguro de que hay muchas personas que están mucho más calificadas para hablar sobre los detalles del modelado de la bomba/tubería que yo, pero mi intención con este artículo está en la metodología, no sobre cómo resolver problemas de tubería/bomba. De todos modos, ¡agradezco abiertamente comentarios o sugerencias de mejora de aquellos que están más conocedores del campo!
El problema
Nos gustaría transferir agua de un tanque a otro. Ya tenemos una bomba y algunas tuberías que se pueden usar para conectar los dos tanques y queremos obtener una estimación de cuánto tiempo llevará transferir toda el agua. Se conoce el volumen de cada tanque, por lo que si podemos estimar el caudal de agua entre los tanques, podemos estimar cuánto tiempo llevará el proceso de transferencia. El aparato completo se muestra a continuación.
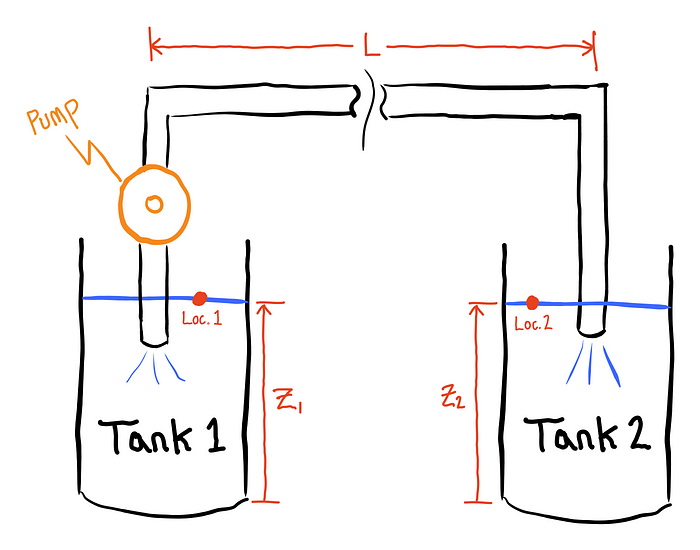
Este problema específico (que puede clasificarse como un problema de "flujo interno") se entiende muy bien dentro del campo de la ingeniería mecánica. Sin embargo, para aquellos menos familiarizados, o en necesidad de una revisión rápida, la forma en que normalmente hacemos resolver estos problemas es con la ecuación de Bernoulli (que se muestra a continuación).
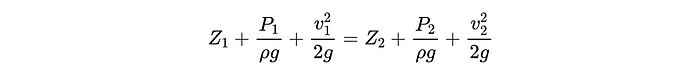La ecuación de Bernoulli es
esencialmente una declaración de conservación de energía que nos dice
cómo la energía de una partícula fluida se transforma entre diferentes
mecanismos de energía a medida que el fluido atraviesa a lo largo de una
línea de flujo (la ruta de flujo que seguiría una partícula imaginaria
si se cae en el fluido). El lado izquierdo de la ecuación representa la
energía total por peso de una partícula de fluido en cualquier primera
ubicación arbitraria (ubicación 1) dentro del fluido, y es la suma de un
término potencial gravitacional, término cinético y término de presión.
A medida que el fluido atraviesa el sistema, la energía debe
conservarse y, por lo tanto, la energía total en cualquier segundo punto
arbitrario (ubicación 2) a lo largo de la línea de corriente
(representada por el lado derecho de la ecuación) debe ser igual a la
energía total en la ubicación 1. 
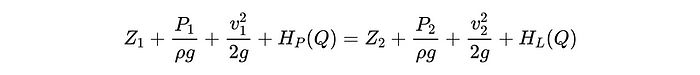
Los términos HP (Q) y HL (Q) representan la cabeza agregada al sistema por una bomba, y la cabeza perdida en el sistema de efectos del mundo real (como fricción, viscosidad, etc.) respectivamente. Tenga en cuenta que ambos términos son funciones de la tasa de flujo de fluido del sistema, Q. (Como consecuencia interesante del párrafo anterior que describe la interpretación de la cabeza, la cabeza de la bomba le dice cuán alta podría una bomba teóricamente empujar un fluido). Examinaremos los términos de bomba y pérdida más a fondo, pero antes de que lo hagamos, simplifiquemos la ecuación anterior para nuestro problema específico.
Mirando el sistema anterior nuevamente, elegiremos convenientemente nuestras dos ubicaciones para la ecuación de Bernoulli, de modo que la mayoría de los términos se cancelen. Podemos hacer esto eligiendo las ubicaciones 1 y 2 para estar en la superficie libre del agua de cada tanque, respectivamente, donde la presión es constante e igual a la presión atmosférica (P1 = P2), y la velocidad es aproximadamente constante y cero (v1 = V2 = 0). También asumiremos que la altura del agua en los dos tanques es la misma en el instante en que estamos analizando el sistema de tal manera que Z1 = Z2. Después de simplificar el álgebra, vemos que casi todos los términos se cancelan, y nos queda el hecho de que la cabeza producida por la bomba debe igualar la cabeza perdida en el sistema debido a las no idealidades. Dicho de otra manera, la bomba está compensando cualquier pérdida de energía en el sistema.
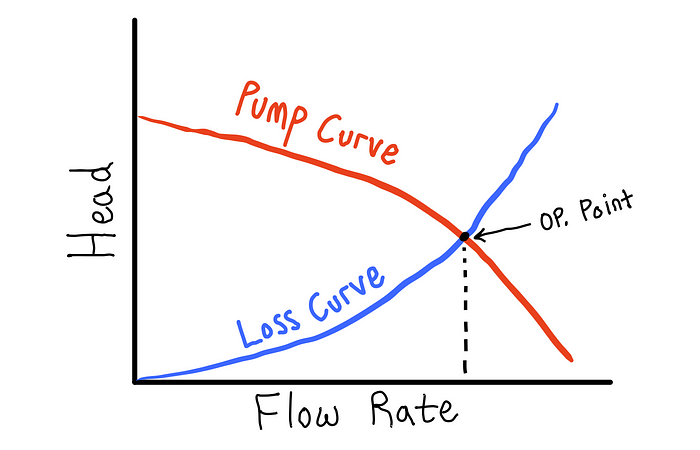
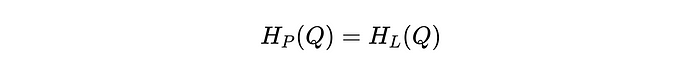Esta situación se puede ver
cualitativamente en la figura a continuación. La cabeza producida por
una bomba disminuye al aumentar la velocidad de flujo, mientras que las
pérdidas en un sistema de tuberías aumentan al aumentar la velocidad de
flujo. El punto donde las dos curvas se cruzan (cabeza de la bomba =
pérdida de cabeza) determina el punto de operación (caudal) del sistema.
El último paso antes de que podamos saltar al código es plantear el problema como un problema de búsqueda de raíces. Restando el lado derecho de la ecuación del lado izquierdo, obtenemos el problema de resolución de raíces que estamos buscando. Es decir, hemos planteado nuestro problema de la siguiente manera: encuentre la velocidad de flujo (q) de modo que el lado izquierdo de la ecuación a continuación sea igual a cero. En este punto, el cabezal de la bomba igualará las pérdidas de la cabeza del sistema.
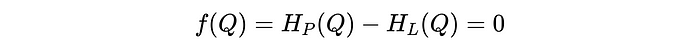
El código
Para evitar perder el panorama general de lo que estamos haciendo, no voy a explicar cada pequeño detalle del código (supongo que ya tiene un fondo razonable en Python). En cambio, voy a enfocar mis esfuerzos en garantizar que la narración y la estructuración del código sea clara, y entrar en más detalles según sea necesario. Como siempre, siéntase libre de hacer cualquier pregunta si algo no está claro.
Configuración
Comenzaremos importando todos los módulos necesarios. Se volverá evidente cómo cada uno de los módulos se usa más adelante, pero vale la pena señalar que las declaraciones de importación clave son las de SciPy. Estas son las funciones que son específicas del problema en cuestión. El bloque de código también establece algunas configuraciones de trazado predeterminadas (al gusto personal), crea una carpeta para guardar las figuras generadas y define algunas constantes de conversión de unidades que facilitan nuestra vida más adelante en el código.
>>from dataclasses import dataclass
>>from pathlib import Path
>>import numpy as np
>>import matplotlib.pyplot as plt
>>import pandas as pd
>>#these are the key libraries for solving the problem
>>from scipy.interpolate import interp1d
>>from scipy.optimize import root_scalar
>>#set plotting defaults
>>plt.style.use('seaborn-v0_8-darkgrid')
>>plt.rcParams['font.family'] = 'Times New Roman'
>>plt.rcParams['font.size'] = 12
>>figsize = (6.4,4)
>>#make folder to save plots to
>>plots_folder = Path('plots')
>>plots_folder.mkdir(exist_ok=True)
>>#define conversion constants for ease of use later
>>INCHES_TO_METERS = 25.4/1000
>>FEET_TO_METERS = 12*INCHES_TO_METERS
>>GALLONS_TO_M3 = 0.0037854118 #convert gallons to m^3
A continuación haremos una pitón dataclass
que esencialmente actúa como un contenedor para almacenar propiedades
de fluidos (densidad, viscosidad y gravedad). Por defecto, las
propiedades se establecen en las de agua. Tenga en cuenta que, aunque no
es completamente necesario, las clases de datos de Python son
increíblemente convenientes. Si son nuevos para usted, le recomiendo que
consulte este video .
>>@dataclass
>>class Fluid():
>> #fluid defaults to water properties
>> rho: float = 997 #kg/m^3
>> mu: float = 0.0007972 #N-s/m^2 = kg/m-s
>> g: float = 9.81 #m/s^2Modelo de tubería
El siguiente paso es modelar las pérdidas de cabeza de la tubería (el término HL (Q) en la ecuación de Bernoulli extendida anterior). Esto generalmente se hace utilizando la ecuación de Darcy-Weisbach que se muestra a continuación, donde F es un factor de fricción (más sobre esto en breve), V es la velocidad de flujo, G es la gravedad, y L y D son la longitud y el diámetro de la tubería, respectivamente.
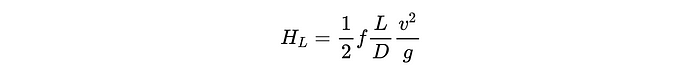
Desafortunadamente, el factor de fricción (F) no es constante, pero también depende de la velocidad del flujo, las propiedades del fluido y las dimensiones de la tubería. Existen varios modelos para calcular F, pero usaremos la ecuación de Haaland, que se muestra a continuación.
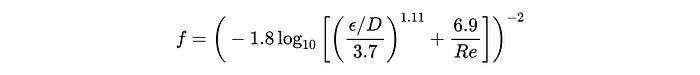En esta ecuación, Epsilon es la
rugosidad de la superficie de la tubería (que se puede encontrar en las
tablas de libros de texto de ingeniería), y RE es el famoso número de
Reynolds, calculado como a continuación.
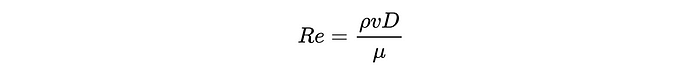Por último, podemos tener en
cuenta que el volumen barrido por unidad de tiempo o la velocidad de
flujo volumétrico (Q) es igual al área de sección transversal (a) de la
tubería de la velocidad del flujo (V). Por lo tanto, dada una velocidad
de flujo en la tubería, podemos calcular la velocidad del flujo
correspondiente en la tubería como:
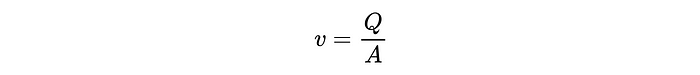
Esperemos
que todas estas ecuaciones no estén rentando el panorama general, solo
estamos buscando un modelo particular de pérdida de la cabeza en una
tubería. Dada una tasa de flujo y las dimensiones de la tubería, primero
calcule la velocidad del flujo correspondiente, luego conéctelo a
través de las ecuaciones anteriores para calcular la pérdida de cabeza
de la tubería. Esto es exactamente lo que el Pipe La clase (que se muestra a continuación) implementa.
El
método de inicialización almacena las dimensiones de las tuberías
(todas que se supone que están en metros) y propiedades de fluido. El A El método calcula el área de sección transversal de la tubería (para aquellos que no están familiarizados con el @property decorador, este artículo lo explica muy bien). El Q_to_v El método convierte el caudal en galones por minuto (GPM) a una velocidad de flujo en m/s. El friction_factor El método evalúa la ecuación de Haaland como se describió anteriormente, y el head_lossy head_loss_feet Evalúe la pérdida de cabeza de la tubería en metros y pies respectivamente (usando la ecuación de Darcy-Weisbach).
>>class Pipe():
>> def __init__(self, L, D, epsilon, fluid: Fluid):
>> #pipe dimensions are all assumed to be in meters
>> self.L = L
>> self.D = D
>> self.epsilon= epsilon
>> #fluid properties
>> self.fluid = fluid
>> @property
>> def A(self):
>> """computes cross-sectional area of pipe in m^2"""
>> return np.pi*(self.D/2)**2 #area in m^2
>> def Q_to_v(self, gpm):
>> """Converts gpm to fluid speed in pipe in m/s"""
>> Q = gpm*GALLONS_TO_M3/60 #flow rate in m^3/s
>> return Q/self.A #flow velocity in m/s
>> def friction_factor(self, gpm):
>> """computes Darcy friction factor, given flow rate in gpm
>> This method uses Haaland's equation, wich is an explicit approximation
>> of the well-known, but implicit Colebrook equation
"""
>> #first get flow velocity from flow rate and pipe dimensions
>> v = self.Q_to_v(gpm)
>> #compute Reynold's number
>> Re = self.fluid.rho*v*self.D/self.fluid.mu
>> #compute relative roughness
>> e_over_d = self.epsilon/self.D
>> #use Haaland's equation
>> f = (-1.8*np.log10((e_over_d/3.7)**1.11 + 6.9/Re))**-2
>> return f
>> def head_loss(self, gpm):
"""computes head loss in meters, given flow rate in gpm"""
>> #get flow velocity
>> v = self.Q_to_v(gpm)
>> #get Darcy friction factor
>> f = self.friction_factor(gpm)
>> #compute head loss in meters
>> hl = 0.5*f*(self.L/self.D)*v**2/self.fluid.g
>> return hl
>> def head_loss_feet(self, gpm):
"""computes head loss in feet, given flow rate in gpm"""
>> hl_meters = self.head_loss(gpm)
>> return hl_meters/FEET_TO_METERSVeamos la clase de tubería en acción. Primero, podemos crear un Fluid objeto para agua y un Pipe Objeto que tiene 100 pies de largo y 1.25 pulgadas de diámetro.
>>#create fluid object for water
>>water = Fluid()
>>#create pipe segment with water flowing in it
>>pipe = Pipe(L=100*FEET_TO_METERS,
>> D=1.25*INCHES_TO_METERS,
>> epsilon=0.00006*INCHES_TO_METERS,
>> fluid=water)A continuación, trazaremos la curva de pérdida de cabeza en función del caudal en GPM. ¿No es increíble lo limpio y fácil que se vuelve el siguiente código cuando explotamos la programación orientada a objetos?
>>gpm_arr = np.linspace(1,30,100)
>>hl = [pipe.head_loss_feet(gpm) for gpm in gpm_arr]
>>fig, ax = plt.subplots(figsize=figsize)
>>ax.plot(gpm_arr, hl)
>>ax.set_xlabel('Flow Rate [gpm]')
>>ax.set_ylabel('Head Loss [ft]')
>>fig.tight_layout()
>>fig.savefig(plots_folder/'pipe_loss_curve.png')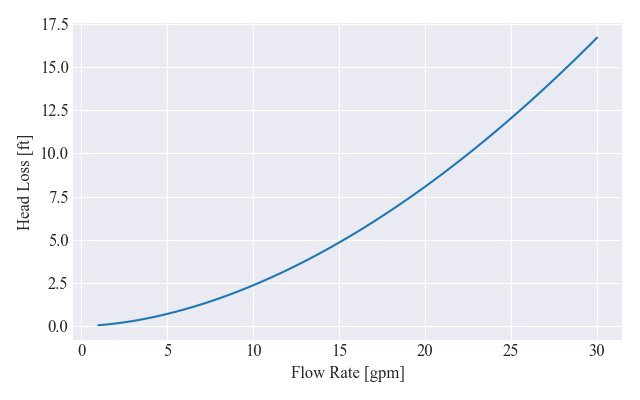
Modelo de bomba
Tenemos un modelo de trabajo de las pérdidas de cabeza de tubería, ahora necesitamos un modelo de la cabeza producido por una bomba, HP (Q). Estoy seguro de que hay modelos analíticos que se pueden usar para determinar un comportamiento de las bombas, pero asumiremos que ya tenemos una bomba específica, a saber, la siguiente bomba de caballos fraccionaria aleatoria que encontré en línea :
La mayoría de las bombas tendrán una hoja de datos que incluye una curva de bomba correspondiente que caracteriza el comportamiento de las bombas. Para nuestra bomba, obtenemos la curva de la bomba a continuación (tenga en cuenta que por razones de derechos de autor, esta es una recreación de la figura proporcionada por el fabricante: el original se puede encontrar aquí ).
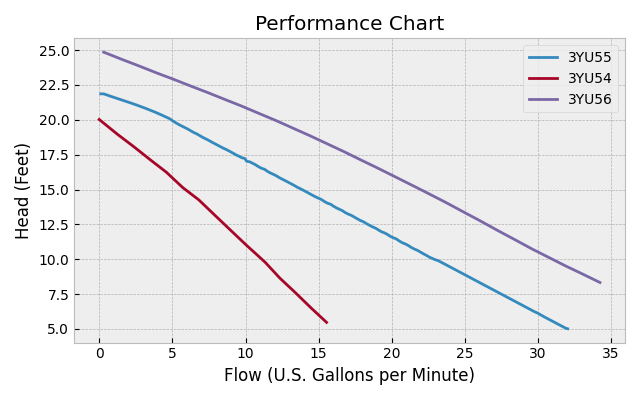
En este punto, tenemos una imagen que representa el comportamiento de las bombas, pero no un modelo matemático que realmente pueda usarse para determinar cómo funcionará en el sistema. Este problema surge todo el tiempo, y la forma en que lo sigo es 1) digitalizar los datos, y luego 2) envolver los datos discretos con un esquema de interpolación para producir una función continua. Déjame ilustrar.
Paso 1) Hay muchas herramientas que existen para digitalizar los datos de imágenes: mi favorito personal es el Utilitiony WebLotDigitizer . Se carga en la imagen de interés de la parcela, alinee los ejes y luego extrae las curvas de datos deseadas (ya sea manualmente o con la herramienta de extracción automática). Los datos se pueden exportar a un archivo .csv.
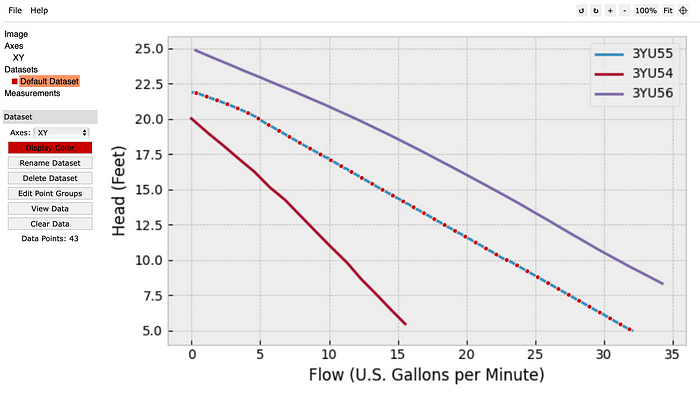
Paso
2) Ahora que tenemos datos digitalizados, solo necesitamos envolverlo
con algún tipo de interpolador, esto es exactamente lo que el Pipe
La clase hace a continuación. El método de inicialización toma el
nombre del archivo .csv, almacena el nombre del archivo, carga los datos
en un Pandas DataFrame, almacenándolo en un data atribuir y luego pasar los datos al interp1d función de scipy. El interp1d
La función luego genera una nueva función que, por defecto, utiliza la
interpolación lineal para convertir los puntos de datos discretos en una
función continua (documentación completa para interp1d La función se puede encontrar aquí ). La función de interpolación recién generada se almacena en un _interp atributo para el acceso posterior. El Pipe La clase también contiene un bounds
método que devuelve una lista que contenga los valores min/max de la
velocidad de flujo en los datos de la curva de la bomba (esto se
utilizará en el algoritmo de búsqueda de raíz) y un head_gain_feet método que toma el caudal en GPM y llama a la función de interpolación subyacente que fue generada por interp1d.
>>class Pump():
>> def __init__(self, file):
>> #store file name
>> self.file = file
>> #read data into pandas dataframe and assign column names
>> self.data = pd.read_csv(file, names=['gpm', 'head [ft]']).set_index('gpm')
>> #create continuous interpolation function
>> self._interp = interp1d(self.data.index.to_numpy(), self.data['head [ft]'].to_numpy())
>> @property
>> def bounds(self):
>> """returns min and max flow rates in pump curve data"""
>> return [self.data.index.min(), self.data.index.max()]
>> def head_gain_feet(self, gpm):
>> """return head (in feet) produced by the pump at a given flow rate"""
>> return self._interp(gpm)Podemos crear un Pump Objeto y mire los datos sin procesar en los que hemos leído.
>>pump = Pump('pump_data.csv')
>>pump.data.head()
También podemos trazar los datos de la curva de la bomba con la curva de pérdida de tubería para ver visualmente dónde funcionará el sistema.
>>head_loss = [pipe.head_loss_feet(gpm) for gpm in pump.data.index]
>>fig, ax = plt.subplots(figsize=figsize)
>>ax.plot(pump.data, label='Pump Curve')
>>ax.plot(pump.data.index, head_loss, label='Pipe Head Loss')
>>ax.set_xlabel("Flow Rate [gpm]")
>>ax.set_ylabel("Head [ft]")
>>ax.legend(frameon=True, facecolor='w', framealpha=1, loc=6)
>>fig.tight_layout()
>>fig.savefig(plots_folder/'pump_curve_with_losses.png')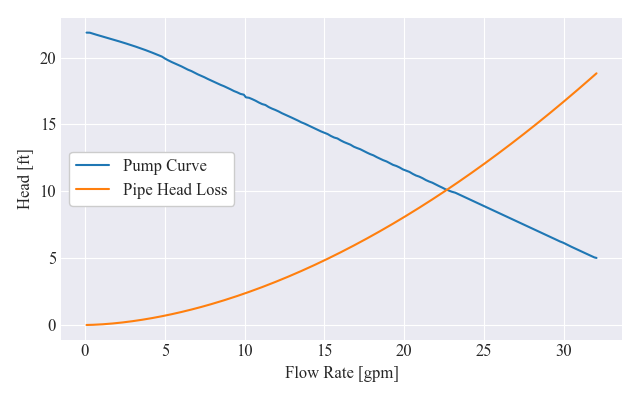
Modelo de sistema
Finalmente
tenemos la infraestructura en su lugar para resolver el punto de
funcionamiento del sistema de bomba/tubería. El último paso es crear un System clase que toma un Pipey Pump objeto y realiza la operación de resolución de raíces. Como se puede ver en el código a continuación, el System La clase toma y almacena un Pipey Pump objeto. Luego usa los dos objetos para crear un residual Método que calcula la diferencia entre el cabezal de la bomba y la pérdida de la cabeza de la tubería. Este residual el método se usa luego en el get_operating_point Método para resolver realmente el punto de funcionamiento del sistema. El método envuelve el root_scalar Funciona desde SciPy, que actúa como una interfaz para varios algoritmos de resolución de raíces. Dejaremos el root_scalar
Función Elija el algoritmo que considere mejor, pero para ayudarlo,
especificaremos un intervalo de soporte en el que sabemos que la raíz se
encuentra entre. En nuestro caso, este intervalo de corchete son los
límites de flujo superior e inferior de los datos de la curva de la
bomba. Documentación completa en el root_scalar La función se puede encontrar aquí .
Consejo profesional: el proceso de inyección del
PipeyPumpobjetos en elSystemclase (en lugar de que la clase del sistema cree unPipeyPumpEl objeto en la instancia) se llama "inyección de dependencia". Esto generalmente se considera una buena práctica de codificación, ya que hace que el código sea más modular, extensible y más fácil de depurar/probar.
>>class System():
>> def __init__(self, pipe: Pipe, pump: Pump):
>> self.pipe = pipe
>> self.pump = pump
>> def residual(self, gpm):
"""
>> Computes the difference between the head produced by the pump
>> and the head loss in the pipe. At steady state, the pump head and
>> head loss will be equal and thus the residual function will go to zero
"""
>> return self.pump.head_gain_feet(gpm) - self.pipe.head_loss_feet(gpm)
>> def get_operating_point(self):
>> """solve for the flow rate where the residual function equals zero.
>> i.e. the pump head equals the pipe head loss"""
>> return root_scalar(self.residual, bracket=self.pump.bounds)Creemos un System y corre el get_operating_point Método para observar los frutos de nuestro trabajo. Como puede ver la salida del código, el get_operating point El método simplemente desmonta la salida del root_scalar función, que es un RootResults objeto. Este objeto es esencialmente solo un contenedor que almacena varios atributos, el más importante es el root atributo tal como contiene la solución a nuestro problema.
>>sys = System(pipe, pump)
>>res = sys.get_operating_point()
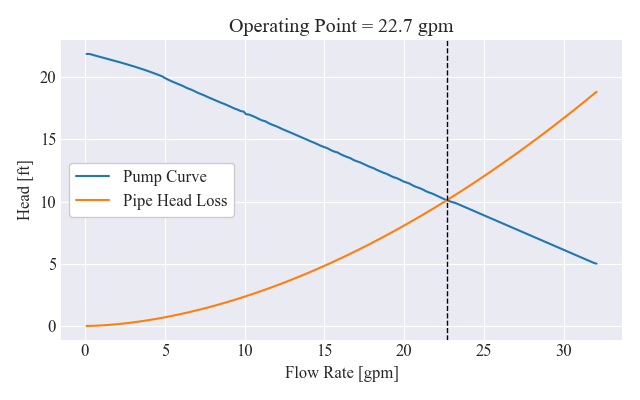
>>res
Podemos trazar la misma bomba y
curvas de pérdida de cabeza nuevamente, esta vez agregando una línea
vertical en el punto de operación calculado de estado estacionario.
>>head_loss = [pipe.head_loss_feet(gpm) for gpm in pump.data.index]
>>fig, ax = plt.subplots(figsize=figsize)
>>ax.plot(pump.data, label='Pump Curve')
>>ax.plot(pump.data.index, head_loss, label='Pipe Head Loss')
>>#plot vertical line at operating point
>>ax.axvline(res.root, color='k', ls='--', lw=1)
>>ax.legend(frameon=True, facecolor='white', framealpha=1, loc=6)
>>ax.set_xlabel("Flow Rate [gpm]")
>>ax.set_ylabel("Head [ft]")
>>ax.set_title(f'Operating Point = {res.root:.1f} gpm')
>>fig.tight_layout()
>>fig.savefig(plots_folder/'intersection_solution.png')
¡Voila! Hemos determinado programáticamente el punto de operación de nuestro sistema. Y debido a que lo hemos hecho usando un marco de codificación algo genérico, ¡podemos probar fácilmente el mismo análisis usando diferentes bombas o tuberías! Incluso podríamos extender nuestro código para incluir múltiples bombas o varios accesorios de tubería/ramas de tubería.
Exploración de diseño
Como
un pequeño ejemplo final, destacando los beneficios de configurar el
código como lo hicimos, realizaremos una exploración de diseño. Usando
la misma bomba, nos gustaría comprender los impactos que tiene la
longitud de la tubería en el caudal volumétrico del sistema. Para hacer
esto, simplemente recorre una matriz de longitudes de tubería (que van
desde 100 a 1000 pies), actualicamos el atributo de longitud del Pipe objeto almacenado en el System,
y luego vuelva a competir el punto de funcionamiento del sistema,
agregando el resultado a una lista. Finalmente, trazamos la tasa de
flujo de agua en función de la longitud de la tubería.
>>#sweep pipe length from 100 to 1000 feet
>>lengths_feet = np.linspace(100, 1000, 1000)
>>lengths_meters = lengths_feet*FEET_TO_METERS
>>flow_rates = []
>>for l in lengths_meters:
>> #update pipe length
>> sys.pipe.L = l
>> #compute new flow rate solution
>> res = sys.get_operating_point()
>> #append solution to flow rates list
>> flow_rates.append(res.root)
>>#plot results
>>fig, ax = plt.subplots(figsize=figsize)
>>ax.plot(lengths_feet, flow_rates)
>>ax.set_xlabel("Pipe Length [ft]")
>>ax.set_ylabel("Flow Rate [gpm]")
>># ax.set_ylim(bottom=0)
>>fig.tight_layout()
>>fig.savefig(plots_folder/'flow_vs_pipe_length.png')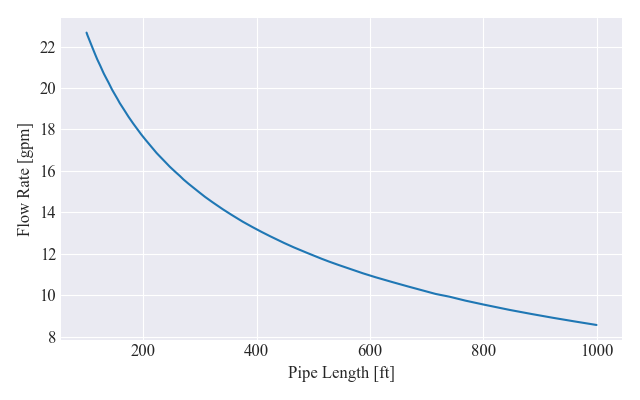
En unas pocas líneas de código, pudimos extraer una visión significativa del comportamiento de nuestro sistema. Si este fuera un problema de diseño, estas ideas podrían impulsar las opciones de diseño clave.
Conclusión
Este artículo, aunque se centró fuertemente en un problema de ejemplo específico de dominio, destaca algunos aspectos de un flujo de trabajo que termino usando mucho. El problema del análisis de puntos operativos surge constantemente en ingeniería y ciencia, y aunque hay muchas maneras de abordar el problema, algunos métodos son más robustos, extensibles y flexibles que otros. La metodología (principios de formulación de problemas y estructuración de código) utilizadas en este artículo me ha servido increíblemente bien, ¡y espero que otros se inspiraran para adoptar un flujo de trabajo similar!
Siéntase libre de dejar cualquier comentario o pregunta que pueda tener o conectarse conmigo en LinkedIn: estaría más que feliz de aclarar cualquier punto de incertidumbre. Finalmente, le animo a que juegue con el código usted mismo (o incluso lo use como plantilla inicial para sus propios flujos de trabajo): el cuaderno Jupyter para este artículo se puede encontrar en mi Github .
Nicholas Hemenway
- Si disfrutaste esto, por favor, me siguen en medio
- Considere suscribirse a las actualizaciones de correo electrónico
- ¿Interesado en colaborar? Vamos a conectarnos en LinkedIn
No hay comentarios.:
Publicar un comentario