Convierte los valores de data a flotantes y calcula la media aritmética.
Esta función se ejecuta más rápido que mean() y siempre retorna un float. data puede ser una secuencia o un iterable. Si el conjunto de datos de entrada está vacío, se lanza una excepción StatisticsError.
>>fmean([3.5, 4.0, 5.25]) # se utiliza fmean para calcular la medina de la lista >>>4.25 # el resultado de la medina.
La ponderación es opcional. Por ejemplo, un profesor asigna una nota a un curso ponderando
las pruebas en un 20%, los deberes en un 20%, un
un examen parcial en un 30% y un examen final en un 30%:
>>grades = [85, 92, 83, 91] >>weights = [0.20, 0.20, 0.30, 0.30] >>fmean(grades, weights) >>>87.6
Si se proporciona weights, debe tener la misma longitud que los data o se producirá
un ValueError.
Convierte los valores de data a flotantes y calcula la media geométrica.
La media geométrica indica la tendencia central o valor típico de data utilizando el producto de los valores (en oposición a la mediaaritmética, que utiliza su suma).
Lanza una excepción StatisticsError si el conjunto de datos de entrada está vacío, o si contiene un cero o un valor negativo. data puedeser una secuencia o un iterable.
No se toman medidas especiales para garantizar que el resultado sea completamente preciso. (Sin embargo, esto puede cambiar en unaversión futura.)
statistics.harmonic_mean(data, weights=None)
Return the harmonic mean of data, a sequence or iterable of real-valued numbers. If weights is omitted or None, then equalweighting is assumed.
La media armónica es recíproco de la mean() aritmética de los recíprocos de los datos. Por ejemplo, la media armónicade tres valores a, b and c es equivalente a 3/(1/a + 1/b + 1/c). Si alguno de los valores es cero, el resultado va a ser cero.
La media armónica es un tipo de promedio, una medida de la tendencia central de los datos. Generalmente es adecuada para calcularpromedios de tasas o fracciones, por ejemplo, velocidades.
Supongamos que un automóvil viaja 10 km a 40 km/h, luego otros 10 km a 60 km/h. ¿Cuál es su velocidad media?
>>harmonic_mean([40, 60]) >>>48.0Supongamos que un un automóvil viaja 5 km a 40 km/h, y cuando el tráfico se despeja, acelera a 60 km/h durante los 30 km restantes del viaje. ¿Cuál es su velocidad media?
>>harmonic_mean([40, 60], weights=[5, 30]) >>>56.0
Una excepción StatisticsError es lanzada si data está vacío, algún elemento es menor que cero, o si la suma ponderada no es positiva.
El algoritmo actual tiene una salida anticipada cuando encuentra un cero en la entrada. Esto significa que no se comprueba la validez de las entradas posteriores al cero. (Este comportamiento puede cambiar en el futuro.)
La idea básica es suavizar los datos utilizando una función de núcleo . para ayudar a dibujar inferencias sobre una población de una muestra.
El grado de suavizado se controla mediante el parámetro de escala H que se llama ancho de banda. Los valores más pequeños enfatizan el local Características, mientras que los valores más grandes dan resultados más suaves.
El núcleo determina los pesos relativos de los datos de la muestra agujas. En general, la elección de la forma del núcleo no importa por mucho que el parámetro de suavizado de ancho de banda más influyente.
Los núcleos que dan algo de peso a cada punto de muestra incluyen Normal ( Gauss ), logístico y sigmoide .
Núcleos que solo dan peso a puntos de muestra dentro del ancho de banda incluir rectangular ( uniforme ), triangular , parabólico ( Epanechnikov ), Cuartic ( bifeal ), tri -peso y coseno .
Si la acumulativa es verdadera, devolverá una función de distribución acumulativa.
A StatisticsError se planteará si la de datos está vacía.
Wikipedia tiene un ejemplo
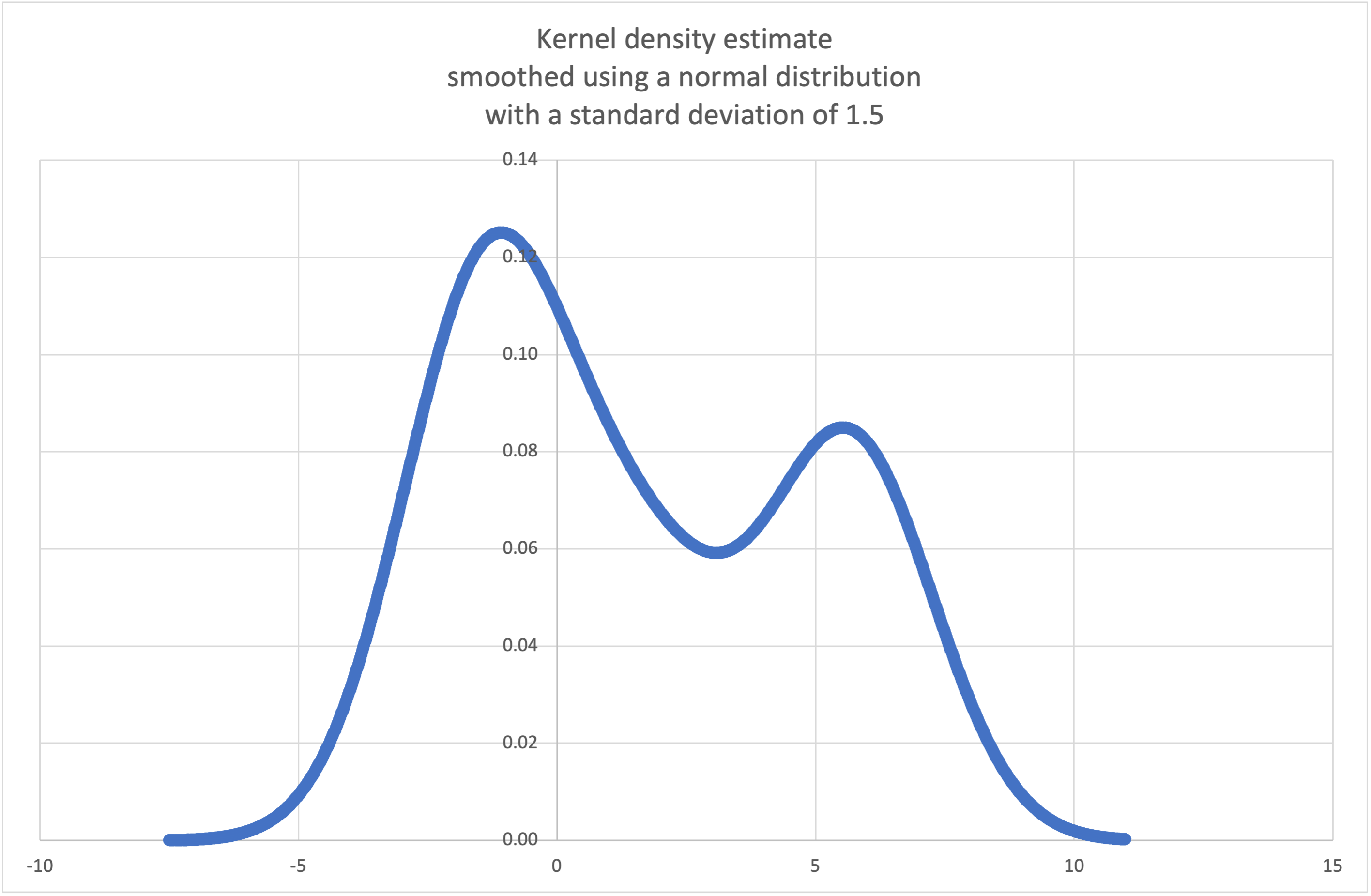
donde podemos usar kde() generar y trazar una probabilidad
función de densidad estimada a partir de una pequeña muestra:
>>sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2] >>f_hat = kde(sample, h=1.5) >>xarr = [i/100 for i in range(-750, 1100)] >>yarr = [f_hat(x) for x in xarr]
Los puntos dexarryyarrpueden utilizarse para hacer una gráfica de la función de densidad
de probabilidad:
statistics.kde_random(data, h, kernel='normal', *, seed=None)
Devolver una función que realice una selección aleatoria de lo estimado
función de densidad de probabilidad producida por kde(data, h, kernel).
Proporcionar una semilla permite selecciones reproducibles. En el futuro, el Los valores pueden cambiar ligeramente a medida que las estimaciones de CDF inversa del núcleo más precisas se implementan. La semilla puede ser un entero, flotador, str o bytes.
A StatisticsError se planteará si la de datos está vacía.
Continuando con el ejemplo de kde(), podemos usar
kde_random() generar nuevas selecciones aleatorias a partir de un
Función de densidad de probabilidad estimada:
>>data = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]>>rand = kde_random(data, h=1.5, seed=8675309)>>new_selections = [rand() for i in range(10)]>>[round(x, 1) for x in new_selections] >>>[0.7, 6.2, 1.2, 6.9, 7.0, 1.8, 2.5, -0.5, -1.8, 5.6]
statistics.median(data)
Retorna la mediana (valor central) de los datos numéricos, utilizando el método clásico de «media de los dos del medio». Si data está vacío, se lanza una excepción StatisticsError. data puede ser una secuencia o un iterable.
La mediana es una medida de tendencia central robusta y es menos sensible a la presencia de valores atípicos que la media. Cuando el número de casos es impar, se retorna el valor central:
>>median([1, 3, 5]) >>>3
Cuando el número de observaciones es par, la mediana se interpola calculando el promedio de los dos valores centrales:
>>>4.0
Este enfoque es adecuado para datos discretos, siempre que se acepte que la mediana no es necesariamente parte de las observaciones.
Si los datos son ordinales (se pueden ordenar) pero no numéricos (no se pueden sumar), considera usar median_low() o median_high() en su lugar.
statistics.median_low(data)
Retorna la mediana baja de los datos numéricos. Se lanza una excepción StatisticsError si data está vacío. data puede ser una secuencia o un iterable.
La mediana baja es siempre un valor presente en el conjunto de datos. Cuando el número de casos es impar, se retorna el valor central. Cuando el número de casos es par, se retorna el menor de los dos valores centrales.
>>median_low([1, 3, 5]) >>>3 >>median_low([1, 3, 5, 7]) >>>3Utiliza la mediana baja cuando tus datos sean discretos y prefieras que la mediana sea un valor representado en tus observaciones, en lugar de ser el resultado de una interpolación.
statistics.median_high(data)
- Retorna la mediana alta de los datos. Lanza una excepción
StatisticsErrorsi data está vacío. data puede ser una secuencia o un iterable. La mediana alta es siempre un valor presente en el conjunto de datos. Cuando el número de casos es impar, se retorna el valor central. Cuando el número de casos es par, se retorna el mayor de los dos valores centrales.
>>median_high([1, 3, 5]) >>>3 >>median_high([1, 3, 5, 7]) >>>5Utiliza la mediana alta cuando tus datos sean discretos y prefieras que la mediana sea un valor representado en tus observaciones, en lugar de ser el resultado de una interpolación.
statistics.median_grouped(data, interval=1.0)
Estima la mediana de los datos numéricos que se han agrupado o agrupado alrededor de los puntos medios de intervalos consecutivos de ancho fijo.
Los datos pueden ser iterables de datos numéricos con cada valor que Exactamente el punto medio de un contenedor. Al menos un valor debe estar presente.
El intervalo es el ancho de cada contenedor.
Por ejemplo, la información demográfica puede haber sido resumida en grupos consecutivos de diez años con cada grupo representados Por los puntos medios de 5 años de los intervalos:
>>from collections import Counter >>demographics = Counter({ 25: 172, # 20 to 30 years old 35: 484, # 30 to 40 years old 45: 387, # 40 to 50 years old 55: 22, # 50 to 60 years old 65: 6, # 60 to 70 years old })
El percentil 50 (mediana) es la persona 536 fuera del 1071 cohorte miembro. Esa persona está en el grupo de edad de 30 a 40 años.
El regular median() la función asumiría que todos en el
El grupo de edad tricenario tenía exactamente 35 años. Un más sostenible
suponiendo que los 484 miembros de ese grupo de edad son uniformemente
distribuido entre 30 y 40. Para eso, usamos
median_grouped():
>>data = list(demographics.elements()) >>median(data) >>>35 >>round(median_grouped(data, interval=10), 1) >>>37.5
La persona que llama es responsable de asegurarse de que los puntos de datos estén separados por múltiplos exactos de intervalo . Esto es esencial para obtener un resultado correcto. La función no verifica esta condición previa.
Las entradas pueden ser de cualquier tipo numérico que se pueda coaccionar a un flotador durante El paso de interpolación.
Estadística. modo ( datos )
Retorna el valor más común del conjunto de datos discretos o nominales data .La moda (cuando existe) es el valor más representativo y sirve como medida de tendencia central. Si hay varias modas con la misma frecuencia, retorna la primera encontrada en data . Si deseas la menor o la mayor de ellas, usa min(multimode(data)) o max(multimode(data)). Se lanza una excepción StatisticsError si la entrada data está vacía. mode asume que los datos de entrada son discretos y retorna un solo valor. Esta es la definición habitual de la moda que se enseña en las escuelas:
>>mode([1, 1, 2, 3, 3, 3, 3, 4]) >>>3
La moda tiene la particularidad de ser la única estadística de este módulo que se puede calcular sobre datos nominales (no numéricos):
>>mode(["red", "blue", "blue", "red", "green", "red", "red"]) >>>'red'
Solo se admiten entradas hashables. Para manejar el tipo set,
Considere lanzar a frozenset. Para manejar el tipo list,
Considere lanzar a tuple. Para entradas mixtas o anidadas, considere
Usando este algoritmo cuadrático más lento que solo depende de las pruebas de igualdad:
max(data, key=data.count).
estadística. multimodo ( datos )
Retorna una lista de los valores más frecuentes en el orden en que aparecen en data . Retornará varios resultados en el caso de que existan varias modas, o una lista vacía si data está vacío:
>>multimode('aabbbbccddddeeffffgg') >>>['b', 'd', 'f']>>multimode('') >>>[]
estadística. pstdev ( datos , mu = none )
Retorna la desviación típica poblacional (la raíz cuadrada de la varianza poblacional). Consultar pvariance() para los argumentos y otros detalles.
>>pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75]) >>>0.986893273527251
Estadística. Pvarianza ( datos , mu = ninguno )
Retorna la varianza poblacional de data , que debe ser una secuencia no vacía o un iterable de números reales. La varianza, o momento de segundo orden respecto a la media, es una medida de la variabilidad (o dispersión) de los datos. Una alta varianza indica una amplia dispersión de valores; una varianza baja indica que los valores están agrupados alrededor de la media.
Si el segundo argumento opcional MU , debería ser la población media de los datos . También se puede usar para calcular el segundo momento alrededor Un punto que no es el medio. Si falta o None (el valor predeterminado), La media aritmética se calcula automáticamente.
Utiliza esta función para calcular la varianza de toda la población. Para estimar la varianza de una muestra, la función variance() suele ser una opción mejor. Lanza una excepción StatisticsError si data está vacío.
>>data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25]
>>pvariance(data) >>>1.25
Si ya has calculado la media de tus datos, puedes pasarla como segundo argumento opcional mu para evitar que se tenga que volver a calcular:
>>mu = mean(data)
>>pvariance(data, mu) >>>1.25
Se admiten decimales (Decimal) y fracciones (Fraction):
>>from decimal import Decimal as D
>>pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")]) >>>Decimal('24.815')
>>from fractions import Fraction as F
>>pvariance([F(1, 4), F(5, 4), F(1, 2)]) >>>Fraction(13, 72)
Nota
Esta función retorna la varianza poblacional σ² cuando se aplica a toda la población. Si se aplica solo a una muestra, el resultado es la varianza muestral s², conocida también como varianza con N grados de libertad.
Si se conoce de antemano la verdadera media poblacional μ, se puede usar esta función para calcular la varianza muestral, pasando la media poblacional conocida como segundo argumento. Suponiendo que las observaciones provienen de una selección aleatoria uniforme de la población, el resultado será una estimación no sesgada de la varianza poblacional.
variance() para los argumentos y otros detalles. >>stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75]) >>>1.0810874155219827
estadística. varianza ( datos , xbar = ninguno )
Retorna la varianza muestral de data , que debe ser un iterable de al menos dos números reales. La varianza, o momento de segundo orden respecto a la media, es una medida de la variabilidad (difusión o dispersión) de los datos. Una alta varianza indica que los datos están dispersos; una baja varianza indica que los datos están agrupados estrechamente alrededor de la media.
Si se da el segundo argumento opcional XBAR , debe ser la muestra media de datos . Si falta o None (el valor predeterminado), la media es calculado automáticamente.
Utiliza esta función cuando tus datos sean una muestra de una población. Para calcular la varianza de toda la población, consulta pvariance().
Lanza una excepción StatisticsError si data tiene menos de dos valores.
Ejemplos:
>>data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>variance(data) >>>1.3720238095238095
Si ya ha calculado la media de la muestra de sus datos, puede pasarlo Como el segundo argumento opcional xbar para evitar el recalculación:
>>m = mean(data)
>>variance(data, m) >>>1.3720238095238095
Esta función no comprueba si el valor pasado al argumento xbar corresponde al promedio. El uso de valores arbitrarios para xbar produce resultados imposibles o incorrectos.
La función maneja decimales (Decimal) y fracciones (Fraction):
>>rom decimal import Decimal as D
>>variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")]) >>>Decimal('31.01875')
>>from fractions import Fraction as F
>>variance([F(1, 6), F(1, 2), F(5, 3)]) >>>Fraction(67, 108)
Nota
Esta es la varianza muestral s² con la corrección de Bessel, también conocida como varianza con N-1 grados de libertad. Suponiendo que las observaciones son representativas de la población (es decir, independientes y distribuidas de forma idéntica), el resultado es una estimación no sesgada de la varianza.
Si conoces de antemano la verdadera media poblacional μ, debes pasarla a pvariance() mediante el parámetro mu para obtener la varianza muestral.
>># Decile cut points for empirically sampled data
>>data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110,
100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129,
106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86,
111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95,
103, 107, 101, 81, 109, 104]
>>[round(q, 1) for q in quantiles(data, n=10)] >>>[81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]

No hay comentarios.:
Publicar un comentario