Scipy: Tutorial Basico estadistico

Fuente: https://xiaoganghe-github-io.translate.goog/python-climate-visuals/chapters/data-analytics/scipy-basic.html?_x_tr_sl=en&_x_tr_tl=es&_x_tr_hl=es&_x_tr_pto=tc 

4.1. Tutorial de SciPy

SciPy es la biblioteca principal para computación científica en Python. Proporciona numerosas rutinas numéricas intuitivas y eficientes, como integración numérica, interpolación, optimización, álgebra lineal y estadística . Estas rutinas se componen como subpaquetes específicos para cada tarea SciPy, como scipy.clusterpara cuantificación vectorial/Kmeans scipy.linalgo rutinas de álgebra lineal. Todos SciPylos subpaquetes dependen de NumPy, pero son prácticamente independientes entre sí.

scipy.statsEl módulo contiene una gran cantidad de estadísticas de resumen y frecuencia, distribuciones de probabilidad, funciones de correlación, pruebas estadísticas, estimación de densidad de kernel, funcionalidad cuasi-Monte Carlo, etc.

En este tutorial, cubriremos:

• scipy.stats:Estadística, distribuciones, pruebas estadísticas y correlaciones

• Análisis de valor extremo

La forma estándar de importar NumPy y un subpaquete SciPy es:

>>import numpy as np
>>from scipy import stats
>>print(stats.__name__)

>>scipy.stats

4.1.1. Estadística descriptiva

Cuando disponemos de un nuevo conjunto de datos, necesitamos una vista descriptiva o resumida de los mismos. Esto normalmente se puede lograr mediante dos enfoques principales:

1. El enfoque cuantitativo scipy.stats describe y resume los datos numéricamente mediante estadísticas. En este tutorial,nos centramos en este enfoque

2. El enfoque visual ilustra los datos con gráficos, diagramas, histogramas y otros. Este enfoque se explica en el tutorial de matplotlib.

Existen varias maneras de obtener estadísticas descriptivas del conjunto de datos en Python. Tenga en cuenta que SciPyse establece en función de NumPyy ofrece funcionalidad adicional en comparación con NumPy. Ya existen estadísticas comunes en NumPy(como mean, median, var).

>>A = np.array([[10, 14, 11, 7, 9.5], [8, 9, 17, 14.5, 12],
              [15, 7, 11.5, 10, 10.5], [11, 11, 9, 12, 14]])
>>print(A)

>># Mean (Location Parameter)
>>print("Mean: ", np.mean(A, axis=0))

>># Median (Location Parameter)
>>print("Median: ", np.median(A, axis=0))

>># Variance (Scale Parameter)
>>print("Variance: ", np.var(A, axis=0, ddof=1))  #ddof=1 provides an unbiased estimator of the variance

[[10.  14.  11.   7.   9.5]
 [ 8.   9.  17.  14.5 12. ]
 [15.   7.  11.5 10.  10.5]
 [11.  11.   9.  12.  14. ]]
Mean:  [11.    10.25  12.125 10.875 11.5  ]
Median:  [10.5  10.   11.25 11.   11.25]
Variance:  [ 8.66666667  8.91666667 11.72916667 10.0625      3.83333333]

Para estadísticas más complicadas como iqr, skew, kurtosis, necesitamos utilizar scipy.stats.

# IQR (Scale Parameter)
print("IQR: ", stats.iqr(A, axis=0))

# Skewness (Shape Parameter)
print("Skewness: ", stats.skew(A, axis=0))

# Kurtosis (Shape Parameter)
print("Kurtosis: ", stats.kurtosis(A, axis=0, bias=False))

# You can also quickly get descriptive statistics with a single function
print("Descriptive statistics:\n", stats.describe(A, axis=0))

IQR:  [2.5   3.25  2.375 3.375 2.25 ]
Skewness:  [ 0.54309084  0.24394285  0.80172768 -0.11813453  0.34616807]
Kurtosis:  [ 1.5        -0.41610621  2.53815357 -0.32082096 -0.768431  ]
Descriptive statistics:
DescribeResult(nobs=4, minmax=(array([8. , 7. , 9. , 7. , 9.5]), array([15. , 14. , 17. , 14.5, 14. ])), mean=array([11.   , 10.25 , 12.125, 10.875, 11.5  ]), variance=array([ 8.66666667,  8.91666667, 11.72916667, 10.0625    ,  3.83333333]), skewness=array([ 0.54309084,  0.24394285,  0.80172768, -0.11813453,  0.34616807]), kurtosis=array([-1.        , -1.25548083, -0.86157952, -1.24277613, -1.30245747]))

Como solemos pandasgestionar datos, podríamos usar la función Pandas describe()para obtener una vista instantánea de las estadísticas comunes del DataFrame (o Serie). A continuación, se muestra un ejemplo de resumen de la precipitación diaria.

>>import pandas as pd

>>dr = pd.read_csv('../../assets/data/Changi_daily_rainfall.csv', index_col=0, header=0, parse_dates=True)
>>print(dr.head())
>>print(dr.describe())

            Daily Rainfall Total (mm)
>>Date                                 
>>1981-01-01                        0.0
>>1981-01-02                        0.0
>>1981-01-03                        0.0
>>1981-01-04                        0.0
>>1981-01-05                        0.0
       Daily Rainfall Total (mm)
>>count               14610.000000
>>mean                    5.721629
>>std                    14.194586
>>min                     0.000000
>>25%                     0.000000
>>50%                     0.000000
>>75%                     4.200000
>>max                   216.200000

También podríamos obtener estadísticas específicas operando directamente en el DataFrame. En este caso, se utiliza el estimador insesgado por defecto.

>># Mean (Location Parameter)
>>print(dr.mean())

>># Median (Location Parameter)
>>print(dr.median())

>># Variance (Scale Parameter)
>>print(dr.var())

>># Skewness (Shape Parameter)
>>print(dr.skew())

>># Kurtosis (Shape Parameter)
>>print(dr.kurtosis())

>>Daily Rainfall Total (mm)    5.721629
>>dtype: float64
>>Daily Rainfall Total (mm)    0.0
>>dtype: float64
>>Daily Rainfall Total (mm)    201.486277
>>dtype: float64
>>Daily Rainfall Total (mm)    5.130516
>>dtype: float64
>>Daily Rainfall Total (mm)    40.832293
>>dtype: float64

4.1.2. Distribuciones

scipy.statsContiene muchos objetos para distribuciones de probabilidad, incluidas distribuciones continuas y distribuciones discretas .

• Distribuciones continuas

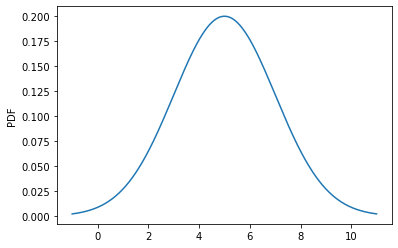
Algunos ejemplos son normla distribución normal, gammala distribución gamma y uniformla distribución uniforme. Cada objeto de distribución continua incluye numerosos métodos útiles, como su función de densidad de probabilidad (PDF), su función de distribución acumulativa (CDF), etc.

Normalmente, importaríamos directamente distribuciones específicas a Python para mayor comodidad. A continuación, se muestra el ejemplo de una distribución normal cuya media es 5 y la desviación estándar es 2.

>>from scipy.stats import norm

>>bins = np.arange(5 - 3 * 2, 5 + 3 * 2, 0.01)

>>PDF = norm.pdf(bins, loc=5, scale=2)  # generate PDF in bins
>>CDF = norm.cdf(bins, loc=5, scale=2)  # generate CDF in bins
>>SF = norm.sf(bins, loc=5, scale=2)  # generate survival function (1-CDF)
>>PPF = norm.ppf(0.5, loc=5, scale=2)  # obtain percent point (inverse of CDF)
>>RVS = norm.rvs(loc=5, scale=2, size=1000)  # generate 1000 random variates
>>MMS = norm.stats(loc=5, scale=2, moments='mvsk')  # obtain the four moments

>>import matplotlib.pyplot as plt

>>plt.plot(bins, PDF)
>>plt.ylabel("PDF")
>>plt.show()

>>plt.plot(bins, CDF)
>>plt.ylabel("CDF")
>>plt.show()

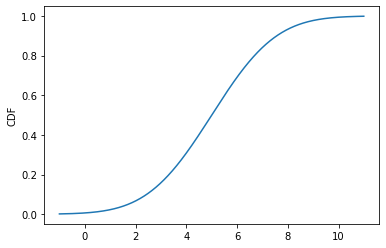
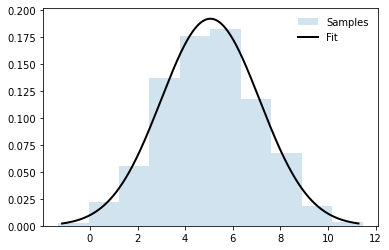
Una práctica común es ajustar un conjunto de datos a una distribución. A continuación, se muestra un ejemplo.

>>samples = norm.rvs(loc=5, scale=2, size=1000)  # pesudo dataset
>>mu, sigma = norm.fit(samples, method="MLE")  # do a maximum-likelihood fit
>>print(mu, sigma)

>># Plot figure
>>bins = np.arange(mu - 3 * sigma, mu + 3 * sigma, 0.01)
>>plt.hist(samples, density=True, histtype='stepfilled',
         alpha=0.2, label='Samples')
>>plt.plot(bins, norm.pdf(bins, loc=mu, scale=sigma),
         'k-', lw=2, label='Fit')
>>plt.legend(loc='best', frameon=False)
>>plt.show()

>>>

5.055650656764304 2.0756534192971463

Nota

Los objetos de distribución scipy.statsse pueden emplear de dos maneras. La primera consiste en introducir los parámetros de distribución cada vez, como en el ejemplo anterior. La otra es crear un objeto de distribución "congelado" fijando los parámetros de distribución. Por ejemplo, . El ejemplo de la siguiente sección sobre distribuciones discretas utiliza este método.distr = norm(loc=5, scale=2)