Matrices en Pyhon para ciencia de datos

 

Guía de referencia: Matrices

Fuente: Coursera & Google

ASÍ COMO has aprendido, NumPy es una potente librería capaz de realizar cálculo numérico avanzado. Una de sus principales ventajas es la posibilidad de trabajar con matrices, ya que una operación aplicada a un vector se ejecuta mucho más rápido que la misma operación aplicada a una lista. El aumento del rendimiento se hace aún más evidente cuando se trabaja con grandes volúmenes de datos. Esta lectura es una guía de referencia para trabajar con arrays NumPy.

Guardar este elemento del curso

Si lo desea, puede guardar una copia de esta guía para futuras consultas. Utilízala como recurso para prácticas adicionales o en tus futuros proyectos profesionales. Para acceder a una versión descargable de este elemento del curso, haga clic en el siguiente enlace y seleccione "Usar plantilla."

Guía de referencia: Arrays

O

Si no dispone de una cuenta de Google, descargue el elemento directamente desde el archivo adjunto que aparece a continuación.

Crear un array

Como has descubierto, para usar NumPy, primero debes importarlo. La práctica estándar es alias como np.

np.array()

Esto crea un ndarray (array n-dimensional). No hay LIMIT en el número de dimensiones que puede tener un array NumPy, pero los arrays con muchas dimensiones pueden ser más difíciles de trabajar.

matriz unidimensional:

>># Crear un array n dimensional

>>import numpy as np

>>array_1d = np.array([1,2,3])

>>array_1d

>>>

array([1, 2, 3])

Observa que un array unidimensional es similar a una lista.

matriz bidimensional:

>># crear un array de 2D

>>import numpy as np

>>array_2d = np.array([[1,2,3],[4,5,6]])

>>array_2d

>>>

array([[1, 2, 3],

       [4, 5, 6]])

Observa que un array bidimensional es similar a una tabla.

matriz tridimensional:

>># crear un array 3D

>>import numpy as np

>>array_3d = np.array([[[1,2],[3,4],[5,6],[7,8]]])

>>array_3d

>>>

array([[[1, 2],

        [3, 4],

        [5, 6],

        [7, 8]]])

Observa que un array tridimensional es similar a dos tablas.

np.ceros()

• Crea una matriz de una forma determinada que se rellena previamente con ceros:

>># crea una matriz que se rellena por ceros de froma predeterminada

>>array_zeros = np.zeros((2,3))

>>array_zeros

>>>

array([[0., 0., 0.], [0., 0., 0.]])

>># Para determinar el tamaño de una matriz se hace con shape >>tamaño_matriz = array_zeros.shape >>tamaño_matriz

>>>

(2, 3)

Se observa que el tamaño de una matriz es (filas, columnas).

np.ones()

• Crea una matriz de una forma determinada que se rellena previamente con unos:

>># crear una matriz de unos

>>array_ones = np.ones((2,2))

>>array_ones

>>>

array([[1., 1.], [1., 1.]])

np.full()

• Y esto crea una matriz de una forma designada que se rellena previamente con un valor especificado:

>># Crear una matriz de ((filas, columnas),numero)

>>array_full = np.full((5,3),8)

>>array_full

>>>

array([[8, 8, 8], [8, 8, 8], [8, 8, 8], [8, 8, 8], [8, 8, 8]])

Estas funciones son útiles para varias situaciones:

• Para inicializar una matriz de un tamaño y forma específicos, y luego llenarla con valores derivados de un cálculo

• Asignar memoria para un uso posterior

• Para realizar operaciones matriciales

Métodos de matrices

Las matrices de NumPy tienen muchos métodos que permiten manipularlas y operar con ellas. Para obtener una lista completa, consulte la documentación sobre matrices de NumPy. Algunos de los métodos más utilizados son los siguientes:

ndarray.flatten()

• Devuelve una copia de la matriz comprimida en una dimensión.

>># ndarray.flatten() devuelve una version comprimida de la matriz en 1 D

>>import numpy as np

>>print(array_2d)

>>ndarray_flatten = array_2d.flatten()

>>print(ndarray_flatten)

>>>

[[1 2 3] [4 5 6]] [1 2 3 4 5 6]

ndarray.reshape()

• Da una nueva forma a un array sin cambiar sus datos.

>># Cambiar la forma de la matriz sin cambiar los datos

>>import numpy as np

>>print(array_2d)

>>print(" ")

>>ndarray_reshape = array_2d.reshape(3,2)

>>print(ndarray_reshape)

>>>

[[1 2 3] [4 5 6]] [[1 2] [3 4] [5 6]]

Añadir un valor de -1 en la nueva forma designada hace que el proceso sea más eficiente, ya que indica a NumPy que infiera automáticamente el valor basándose en otros valores dados.

>># Cambiar la forma de la matriz sin cambiar los datos y agregando un valor de -1 >>import numpy as np >>print(array_2d) >>print(" ") >>ndarray_reshape = array_2d.reshape(3,-1) >>print(ndarray_reshape)

>>>

[[1 2 3] [4 5 6]] [[1 2] [3 4] [5 6]]

ndarray.tolist()

• Esto convierte un array en un objeto lista. Las matrices multidimensionales se convierten en listas anidadas.

>># Convierte un array en un objeto tipo lista

>>import numpy as np

>>print(array_2d)

>>print(" ")

>>ndarray_tolist = array_2d.tolist()

>>print(ndarray_tolist)

>>print(type(ndarray_tolist))

>>>

[[1 2 3] [4 5 6]] [[1, 2, 3], [4, 5, 6]] <class 'list'>

Funciones matemáticas

Los arrays de NumPy también tienen muchos métodos que son funciones matemáticas:

• ndarray.max(): devuelve el valor máximo en la matriz o a lo largo de un eje especificado.

>># ndarray.max() devuelve el valor máximo en la matriz o a lo largo de un eje especificado.

>>import numpy as np

>>print(array_3d)

>>print(" ")

>>ndarray_max = array_3d.max()

>>print(ndarray_max)

>>>

[[[1 2] [3 4] [5 6] [7 8]]] 8

• ndarray.mean(): devuelve la media de todos los valores de la matriz o a lo largo de un eje especificado.

>># ndarray.mean() devuelve la media de todos los valores de la matriz o a lo largo de un eje especificado.

>>import numpy as np

>>print(array_3d)

>>print(" ")

>>ndarray_mean = array_3d.mean()

>>print(ndarray_mean)

>>>

[[[1 2] [3 4] [5 6] [7 8]]] 4.5

• ndarray.min(): devuelve el valor mínimo de la matriz o de un eje especificado.

>># ndarray.min() devuelve el valor mínimo de la matriz o de un eje especificado.

>>import numpy as np

>>print(array_3d)

>>print(" ")

>>ndarray_min = array_3d.min()

>>print(ndarray_min)

>>>

[[[1 2] [3 4] [5 6] [7 8]]] 1

• ndarray.std(): devuelve la desviación estándar de todos los valores de la matriz o a lo largo de un eje especificado.

>># ndarray.std(): devuelve la desviación estándar de todos los valores de la matriz o a lo >>#largo de un eje especificado.

>>import numpy as np

>>print(array_3d)

>>print(" ")

>>ndarray_std = array_3d.std()

>>print(ndarray_std)

>>>

[[[1 2] [3 4] [5 6] [7 8]]] 2.29128784747792

Atributos de las matrices

Las matrices de NumPy tienen varios atributos que permiten acceder a información sobre la matriz. Algunos de los atributos más utilizados son los siguientes:

• ndarray.shape: devuelve una tupla de las dimensiones de la matriz.

• ndarray.dtype: devuelve el tipo de datos del contenido de la matriz.

• ndarray.size: devuelve el número total de elementos de la matriz.

• ndarray.T: devuelve la matriz transpuesta (las filas se convierten en columnas y las columnas en filas).

>>import numpy as np

>>print(array_3d)

>>print(" ")

>>ndarray_shape = array_3d.shape

>>print("la dimension de la matriz es: ",ndarray_shape)

>>print(" ")

>>ndarray_dtype = array_3d.dtype

>>print("El tipo de datos del contenido de la matriz es: ",ndarray_dtype)

>>print(" ")

>>ndarray_size = array_3d.size

>>print("La cantidad de elementos de la matriz es: ",ndarray_size)

>>print(" ")

>>ndarray_t = array_3d.T

>>print("La matriz transpuesta es: ",ndarray_t)

>>>

[[[1 2] [3 4] [5 6] [7 8]]] la dimension de la matriz es: (1, 4, 2) El tipo de datos del contenido de la matriz es: int64 La cantidad de elementos de la matriz es: 8 La matriz transpuesta es: [[[1] [3] [5] [7]] [[2] [4] [6] [8]]]

Indexación y segmentación

Acceda a elementos individuales de una matriz NumPy utilizando indexación y corte. La indexación en NumPy es similar a la indexación en listas de Python, excepto que se pueden usar múltiples índices para acceder a elementos en matrices multidimensionales.

>>import numpy as np >>print(array_3d) >>print(" ") >>print(array_3d[0,0])

>>>

[[[1 2] [3 4] [5 6] [7 8]]] [1 2]

El rebanado también puede usarse para acceder a subarreglos de un arreglo NumPy:

>># Rebanado >>import numpy as np >>a = np.array([(1,2,3),(4,5,6)]) >>print(a) >>print(" ") >>print(a[:,1:])

>>>

[[1 2 3]

 [4 5 6]]

 [[2 3]

 [5 6]]

Operaciones con arrays

Las matrices NumPy soportan muchas operaciones, incluyendo funciones matemáticas y aritméticas. Éstas incluyen la suma y multiplicación de matrices, que realiza aritmética elemento a elemento en matrices:

>># suma de matrices >>a = np.array([(1,2,3),(4,5,6)]) >>b = np.array([(1,2,3),(1,2,3)]) >>c = a + b >>print(c)

>>>

[[2 4 6] [5 7 9]]

Además, hay cerca de 100

funciones matemáticas útiles que se pueden aplicar a matrices individuales o múltiples.

Mutabilidad

Las matrices de NumPy son mutables, pero con ciertas limitaciones. Por ejemplo, un elemento existente de un array puede ser cambiado:

>># Mutabilidad de array >>a = np.array([(1, 2), (3, 4)]) >>a[1][1] = 100 >>a

>>>

array([[ 1, 2], [ 3, 100]])

Sin embargo, el array no puede alargarse o acortarse.

Cómo almacenan los datos en memoria las matrices NumPy

Las matrices NumPy funcionan asignando un bloque contiguo de memoria en el momento de la instanciación. La mayoría de las otras estructuras en Python no hacen esto; sus datos están dispersos por la memoria del sistema. Esto es lo que hace que los arrays de NumPy sean tan rápidos; todos los datos se almacenan juntos en una dirección concreta de la memoria del sistema.

Curiosamente, esto es también lo que impide que un array sea alargado o acortado: La memoria contigua está ocupada por otra información. No hay espacio para más datos en esa dirección de memoria. Sin embargo, los elementos existentes de la matriz pueden sustituirse por otros nuevos.

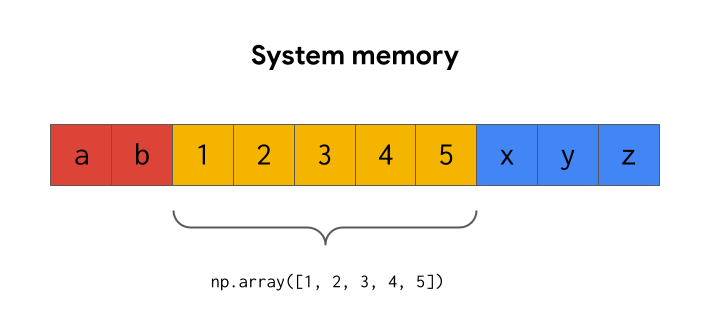
La única forma de alargar un array es copiar el array existente a una nueva dirección de memoria junto con los nuevos datos.